All Creatures MAX, MIN, LARGE and SMALL
This article provides a little insight on when to use the MAX, MIN, LARGE and SMALL functions. By Liam Bastick, director (and Excel MVP) with SumProduct Pty Ltd.
Query
I am a little confused as to when to use MAX, MIN, LARGE and SMALL. When should I use what where and why?
Advice
MAX and MIN are familiar to many Excel users, but it is still probably worth performing a recap using the attached Excel file. MAX does exactly what it says on the tin – it calculates the maximum value in a range:
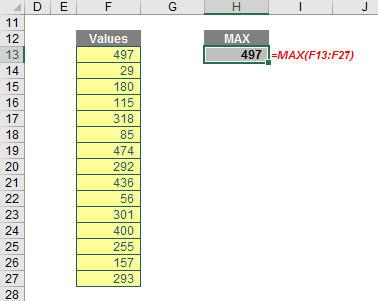
MIN works very similarly but calculates the minimum value. I have underlined value for both of these functions: in fact, all four functions only work on numerical data, so bear this in mind when trying to calculate relative ranking / sizing (more on ranking next month). Even so, modellers frequently make mistakes with MAX (and similar ones with MIN):

These examples highlight that you should be careful with using blanks both in the ranges and in the formulae themselves. Regular readers will notice I often omit zeros in my formulae but with MAX and MIN I will often take care to explicitly use zeros.
Some versions of Excel 2016 have extended MAX and MIN with new functions MAXIFS and MINIFS (please refer to our article on new Excel 2016 functions and features for further details). However, not everyone can use these functions and end users may see #NAME? errors in their spreadsheets if they are opened in earlier versions of Excel. That’s not exactly ideal.
However, you can achieve a similar result combing MAX (or MIN) with IF in an array formula (where the curly braces are not typed but entered using CTRL + SHIFT + ENTER rather than ENTER – please see this article for more information):
{=MAX(IF(Range_Condition,Range))}
Range_Condition is a logical test on the Range: it could be to test for positives, negatives, even numbers, odd numbers, etc.

Once you get the hang of them, they are very easy to construct.
There is a highly relevant finance example combining MAX and MIN functions, namely calculating the maximum dividend allowable for a particular period. Dividends may only be paid out of what are known as distributable reserves (this is a bit of an oxymoron as dividends are also known as distributions). Revaluation reserves, share premium accounts, capital redemption reserves are all non-distributable. Essentially, dividends may only be paid out of the current year’s Net Profit After Tax (NPAT) and the aggregation of all previous year’s profits after past distributions, Retained Earnings. Dividends may not make the Balance Sheet’s Total Equity become negative. This shows insolvency and this sort of distribution is illegal in most territories. Given non-distributable reserves may not become negative allow me to concentrate simply on NPAT and Retained Earnings here.
To derive the maximum dividend allowable, let me consider some scenarios. Let’s imagine the following scenario:

It isn’t rocket science that if Retained Earnings and NPAT are both positive, then the maximum dividend allowed is the sum of the two.
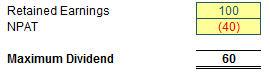
If NPAT is negative, but Retained Earnings are positive and exceed the NPAT figure, then the maximum dividend allowed is the net of the two figures. Should the net be negative, no dividend is allowed.

Here is the one that often surprises people. If Retained Earnings is negative but NPAT is positive, regardless of whether the net is positive or negative, the maximum dividend allowed is the NPAT amount. This may seem incomprehensible upon first thought, but it is typically dependent upon two conditions:
- The company’s auditors must sign off on it. This is to ensure the company is still seen to be a going concern (i.e. it can still continue to operate and trade its way out of any short-term difficulties).
- The shareholders must vote for it. Almost as hilarious as when Members of Parliament solemnly vote for their 50% pay rise each year.
If you think about it some more, this makes sense. Remember, dividends cannot be paid if the company is insolvent. The auditors check to see whether the company can “afford” it for other reasons. But if you don’t allow this scenario how would anyone ever attract share capital for a start-up company? A new company may have to provide for certain factors which may never come to fruition. A large non-current asset may have to be written off as not fit for purpose if a company’s strategy changes without any cash consequence. Is it acceptable that shareholders have to wait 10 years for the Retained Earnings losses to be covered even if the business is hugely profitable in the meantime? No, and this is precisely why this is the rule in many territories.
The next scenario is more obvious:

With both a negative NPAT and Retained Earnings, there is no leeway now. These scenarios seem to suggest the following formula:
=MAX(NPAT + Retained Earnings, NPAT, 0)
This allows for the above scenarios. The check to ensure that the value is non-negative (i.e. the inclusion of zero in the MAX formula) is so that shareholders do not get asked to pay a dividend to the company. I can’t imagine that would go down too well.
We are not done yet though. Let’s go back to the penultimate scenario but now consider the cash position as well:

Here, the Cash Available is the total amount of cash available to pay the dividend. Technically, this includes any cash reserves built up over time, but many companies only consider the cash position for the period the dividend relates to (this is the scenario I shall be modelling in the case study shortly). This seems to suggest the formula:
=MIN(MAX(NPAT + Retained Earnings, NPAT, 0), Cash Available)
Let me just check with slightly revised numbers:

In this scenario, the company is overdrawn. Oops. Here, this company is going to be asking for money again from its shareholders. Not a good idea. This leads to the slightly revised – and finally correct – formula:
Maximum Dividend = MAX(MIN(MAX(NPAT + Retained Earnings, NPAT), Cash Available), 0)

Ah yes, the wonderful MAX(MIN(MAX)) formula. It may not be the prettiest formula in the world, but the point is, it gives the right number.
Now let’s consider LARGE and SMALL. These are similar functions, but require two arguments:
=LARGE(Range,n)
=SMALL(Range,n)
These two functions return the nth largest and smallest values in a given Range. n must be a positive integer less than or equal to the number of non-blank items in the Range. For example,
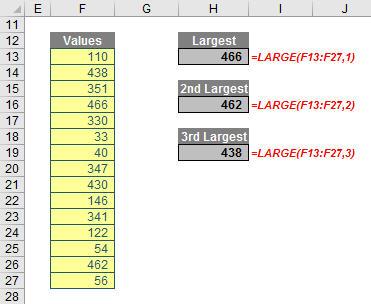
SMALL acts very similarly and comparable examples may be found in the attached Excel file. As with MAX and MIN, there are opportunities to create errors using these reasonably straightforward functions:

Again, other than choosing an inappropriate n (e.g. choosing a negative value, too large a value or a non-integer), blank cells may again cause problems. Please ensure you do not include blank cells in your given Range.
LARGE may be used to rank numerical data in descending order using the ROWS function:
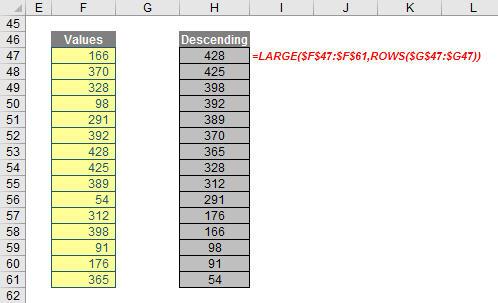
A similar formula using SMALL will create the reverse ordered list (i.e. in ascending order). In both instances, ROWS is used to create a counter which will increase n by one as the formula is copied down column H in my example above.
LARGE and SMALL may also be used to derive statistical data from a range, sometimes requiring an array formula and sometimes not (this is often a case of trial and error for the inexperienced). For example, here’s two ways to calculate the sum of the top three (largest) values in the following range:
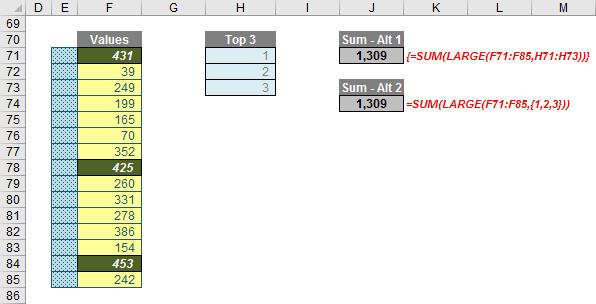
The formulae
{=SUM(LARGE(F71:F85,H71:H73))}
and
=SUM(LARGE(F71:F85,{1,2,3}))
will both sum the top three items in the list. You should note that an array formula is avoided in the second formula as n is specified as {1,2,3} – effectively creating an array of data without pressing CTRL + SHIFT + ENTER.
Similar formulae may be created for the sum of the bottom five, the average of the fourth, eighth and 12th largest items and so on. Try doing that with MAX or MIN!
Word to the Wise
The four functions discussed here all consider numerical data only. Next month, I will look at how to rank data that is non-numerical in nature.
If you have a query for the Spreadsheet Skills section, please feel free to drop Liam a line at liam.bastick@sumproduct.com or visit the SumProduct website.

