Calculating Interest Rates Correctly
Introduction
As a professional modeller for more years than he’d care to admit, Excel MVP and FCA Liam Bastick highlights some of the common mistakes prevalent in financial modelling / Excel spreadsheeting. This article looks at common errors in calculating interest rates correctly.
As a model auditor for over 30 years, you start to recognise and look out for common errors in financial spreadsheets. One common area of malignant modelling is the inability of many analysts to convert an annual interest rate into a monthly or quarterly rate correctly. Sometimes the error is immaterial; other times, it can cause major issues (e.g. for bank forecasts). This isn’t so much an Excel issue as a mathematical problem, but it is still relevant to financial modellers and more often than not, it’s calculated incorrectly.
The key thing any modeller charged with this exercise must do is read the debt term sheet or deposit account prospectus to see what the effective annual rate is. Accountants talk about nominal interest rates and such like, but the effective annual rate is the amount of interest expressed as a percentage of the opening debt or cash balance if interest were to be paid and calculated as per the terms of the underlying document.
It’s easier said than done.
Let me demonstrate with an example: consider a loan of $100 where interest is calculated in arrears on a monthly compounding basis paid quarterly at the end of each quarter. The effective rate is determined to be 12%. The question is, what is the appropriate monthly rate be for cashflow calculations?
Who said 1%? That’s a common answer, derived as 12% divided by the number of months in a year (12). It sounds good, but if I crunch the numbers I will get the following result:
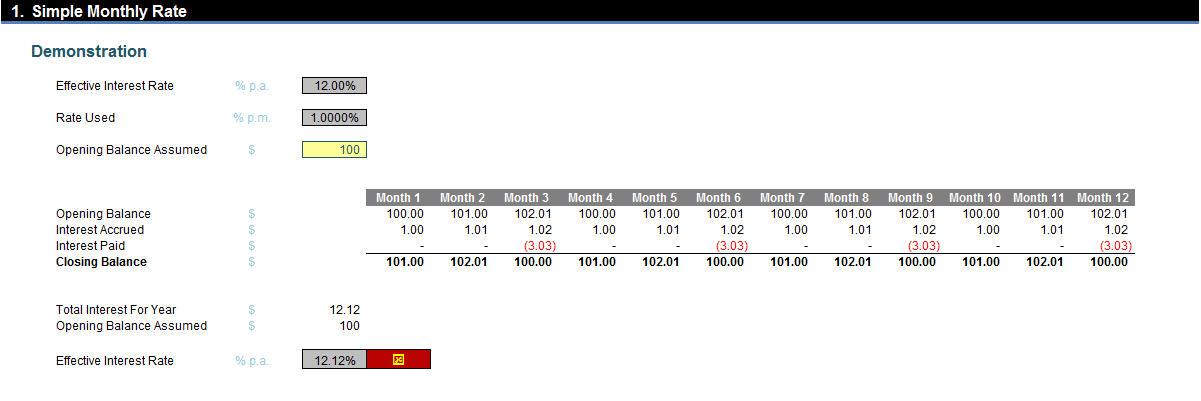
On a $100 balance with interest of 1% monthly paid quarterly, the total interest for the year will be $12.12 – that’s an effective annual rate of 12.12% rather than 12% (12.00%). This is not correct, as interest is being rolled up at the end of each of the first two months in the quarter and is attracting further interest, i.e. interest is compounding and has not been taken into account by simply dividing the annual rate by the number of months in a year.
So, what about using the compounding formula instead? Interest can then be calculated as
=(1+12%)1/12 - 1
This equates to 0.9489% per month. This will take into account compounding – well, sort of:
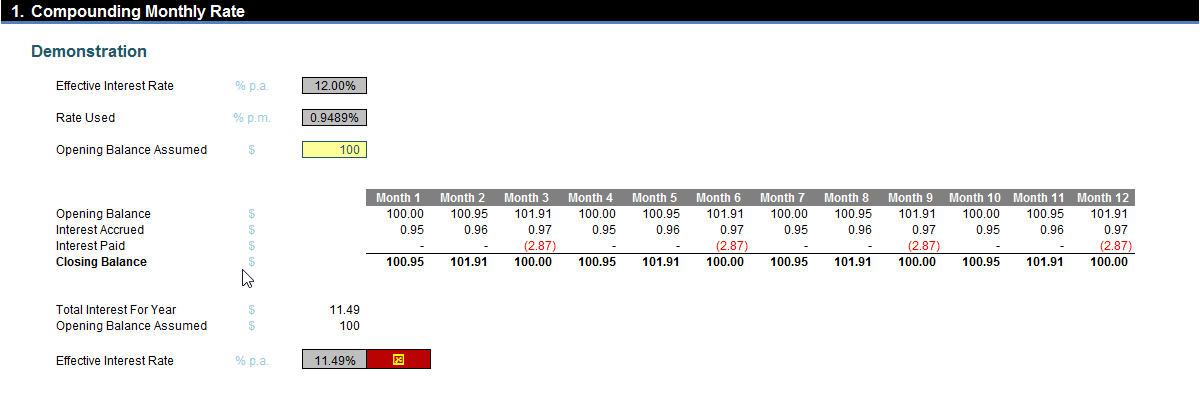
This hasn’t worked either: interest has been under-accrued (that’s a good word I’ve just made up) as only $11.49 has been computed for the year – an effective rate of 11.49%.
Here, the calculation is again too simplistic as it does not take into account that the interest is paid quarterly. This means that compounding throughout the year does not occur, hence the shortfall of 0.51%.
The correct formula is:
=(1+(Effective Annual Interest Rate x Payment Frequency / Months in Year))1/Payment Frequency - 1
If payments are made once every three months then there are four payments (equal to Months in Year / Payment Frequency or 12 / 3) each year. At these points, compounding stops. Therefore, the interest rate of 12% per annum is effectively 3% per quarter. The compounding formula can then be applied to the quarterly rate to get the monthly rate accordingly:
=(1+3%)1/3 - 1
This equates to 0.9902%. This is correct, viz.
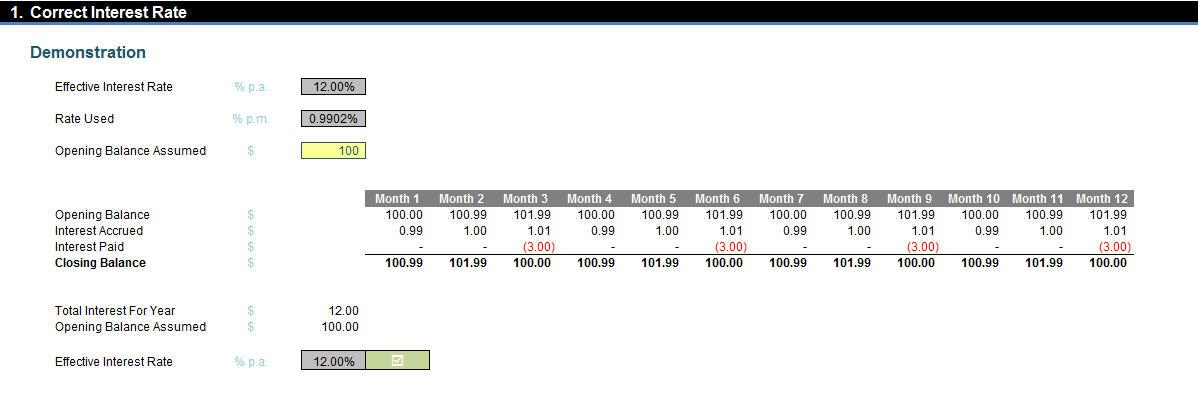
Success!
This is the formula that should be applied to calculate the appropriate monthly interest rate from a quoted effective annual one. The attached Excel file provides examples and a template that may be used.
Word to the Wise
It should be noted that if interest is paid monthly, the formula above reduces to the simple interest rate method (i.e. simply divide the rate by 12). Similarly, if interest is only paid at the end of the year, the compounding formula is correct too. Essentially, the formula explained above is the “halfway house” between the two.
Happy modelling!

