Power Pivot Principles: The A to Z of DAX Functions – GEOMEAN
13 February 2024
In our long-established Power Pivot Principles articles, we continue our series on the A to Z of Data Analysis eXpression (DAX) functions. This week, we look at GEOMEAN.
The GEOMEAN function
The GEOMEANfunction is a statistical function in DAX that calculates the geometric mean of an expression evaluated over a column representing a sample population. The syntax for the GEOMEAN function is as follows:
GEOMEAN(column)
It has one [1] argument:
- column: this represents a column of numbers or expression that evaluated to a column of numbers for which the geometric mean is to be computed.
Before we get into more detail about the function, what is the geometric mean and what is it useful for? The geometric mean is a central tendency function similar to the more commonly known arithmetic mean, or average. However, while the arithmetic mean adds numbers together, the geometric mean multiplies them. This makes the geometric mean more suitable for sets of numbers with widely varying ranges and is especially useful in financial analysis for calculating average rates of return over time.
Example Usage
Imagine you have a table named InvestmentReturns that contains monthly return rates for a particular stock. You could use the GEOMEAN function to calculate the average monthly return rate, which can then be used to analyse the performance of the stock over time.

Taking the above table named InvestmentReturns we can go into the Measures tab and create a new measure called Geomean. Ensuring that the InvestmentReturns table is selected under Table name, the code to get the average monthly return is simply
=GEOMEAN(InvestmentReturns[Return])-1
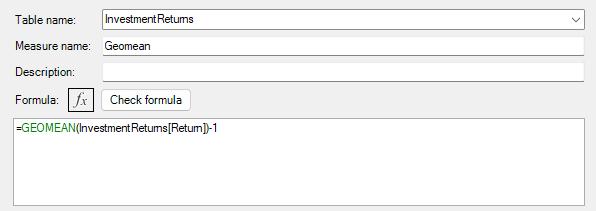
Putting Geomean into a pivot table it gives us the average growth rate of 16.41%.

Here are some key considerations for using GEOMEAN:
- Non-Negative Numbers: The GEOMEAN function is defined only for non-negative numbers. If your data set includes negative numbers, the function will return an error. This is because the geometric mean of negative numbers is not a meaningful statistic.
- Handling Zeroes: While the geometric mean is not defined for sets that include zero, the GEOMEAN function in DAX handles zeroes in the data set. However, remember that including zeroes can drastically affect your geometric mean, as they contribute nothing to the product before taking the nth root (where n is the number of items in your set).
- Usage Scenario: The geometric mean is most appropriate for data sets that describe proportional growth, such as the growth rates of investments. It can also be used to average ratios or percentages.
- Performance: Like any DAX function, the performance of the GEOMEAN function can be affected by the size of the dataset and the complexity of the expressions involved. It's always a good practice to monitor and optimize your DAX expressions for better performance.
Come back next week for our next post on Power Pivot in the Blog section. In the meantime, please remember we have training in Power Pivot which you can find out more about here. If you wish to catch up on past articles in the meantime, you can find all of our Past Power Pivot blogs here.

