Power Pivot Principles: The A to Z of DAX Functions – GCD
16 January 2024
In our long-established Power Pivot Principles articles, we continue our series on the A to Z of Data Analysis eXpression (DAX) functions. This week, we look at GCD.
The GCD function
In mathematics, the greatest common divisor (GCD), also known as the greatest common denominator or the highest common factor, of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder. For example, the GCD of 24 and 18 is 6.

To show this, if we factorise the numbers down to primes:
24 = 2 x 2 x 2 x 3
18 = 2 x 3 x 3
Therefore, the prime numbers shared are:
2 x 3 = 6.
It should be noted that the GCD will also divide the difference between the two (24 – 18 = 6).
A much more efficient method is the Euclidean algorithm, which uses the division algorithm in combination with the observation that the GCD of two numbers also divides their difference:
- Divide 24 by 18 is 1 remainder 6, so
- Divide 18 by 6 is 3 with no remainder.
Therefore, 6 is the GCD of 24 and 18.
The GCD function is one of the Math and Trig functions which use to calculate the greatest common divisor of two integers. It has the following syntax:
GCD(number1, [number2], …)
- number1, number2, …: the number1 is required and any subsequent numbers are optional. We can enter from one [1] to 255 values and if values we enter is not an integer, it will be truncated.
It should be noted that:
- if any argument is nonnumeric, the GCD function will return #VALUE! error
- if any argument is less than zero [0] or a parameter to GCD is >=2^53, the GCD function will return #NUM! error
- a prime number has only itself and one [1] as even divisors
- this function is not supported for use in DirectQuery mode when used in calculated columns or row-level security (RLS) rules.
Let’s consider the following example, where we have this TB_Number Table loaded to the Data Model:

We will write a DAX measure on the calculated column:
GCD_Example := GCD(TB_Number[Value 1],TB_Number[Value 2])

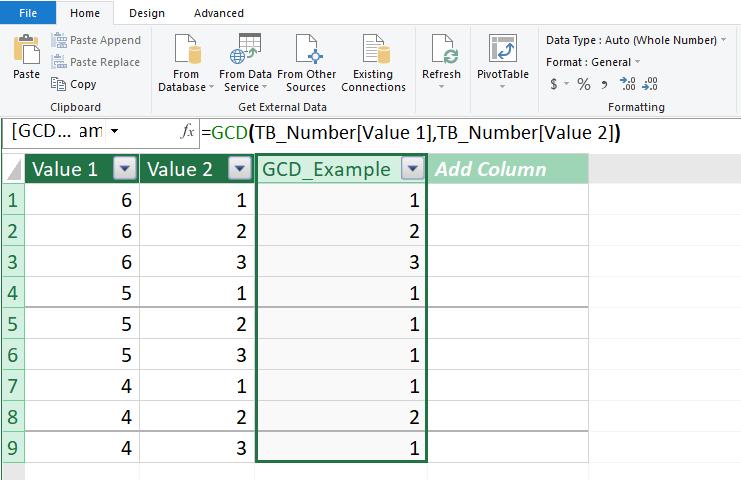
As we can see here all the greatest common divisor is listed out here for Value 1 and Value 2.
Come back next week for our next post on Power Pivot in the Blog section. In the meantime, please remember we have training in Power Pivot which you can find out more about here. If you wish to catch up on past articles in the meantime, you can find all of our Past Power Pivot blogs here.

