Power Pivot Principles: The A to Z of DAX Functions – FACT

In our long-established Power Pivot Principles articles, we continue our series on the A to Z of Data Analysis eXpression (DAX) functions.  This week, we look at FACT. 

The FACT function

Not to be confused with fact tables, the FACT functionis one of the mathematical and trigonometric functions and returns the factorial of a number.  In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. For example, 

The value of 0! is one [1], according to the convention for what is known as an empty product, being the multiplicative identity (just as zero (0) is the additive identity).

The factorial operation is encountered in many areas of mathematics, notably in combinatorics, algebra, and mathematical analysis. Its most basic occurrence is the fact that there are n! ways to arrange n distinct objects into a sequence.  These arrangements are called the permutations of the set of objects. 

These numbers become astronomical (technical term) very quickly. 

It employs the following syntax:

It has one [1] argument:

• number: which is the non-negative number you want the factorial of.

Here are a few remarks about this function:

• the number is shortened, and an error is returned if it is not an integer
• an error is returned if the result is too big
• the maximum factorial that the FACT function may return is 170!
• 21! is the maximum factorial that the FACT function can return without losing precision
• this function is not supported in DirectQuery mode when used in calculated columns or row-level security (RLS) rules.

Let’s consider the following example:

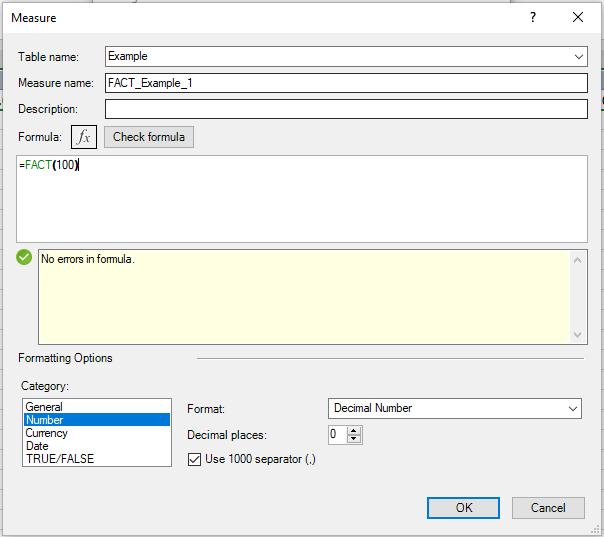
What we have here is a measure for factorial of 100, after we put this result in Pivot Table, we will have the following figure:

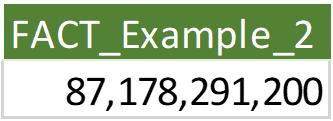
However, as you can see the precision has dropped significantly as mathematically there should only be 24 zeros at the end of the resulting number for factorial of 100.  Let’s consider another value under 21 where precision is still intact:

Thus, we create a factorial of fourteen [14] for our second example which will have the following result:

Come back next week for our next post on Power Pivot in the Blog section.  In the meantime, please remember we have training in Power Pivot which you can find out more about here.  If you wish to catch up on past articles in the meantime, you can find all of our Past Power Pivot blogs here.