Power Pivot Principles: The A to Z of DAX Functions – DURATION

In our long-established Power Pivot Principles articles, we continue our series on the A to Z of Data Analysis eXpression (DAX) functions.  This week, we look at DURATION. 

The DURATION function

The DURATION function is one of the financial functions where it returns that Macaulay duration for an assumed par value of $100.  It is the measure of the weighted average maturity of cash flows.  Each cash flow weight can be found by dividing the present value of the cash flow by the price.  This concept used by portfolio manager.  It has the following formula:

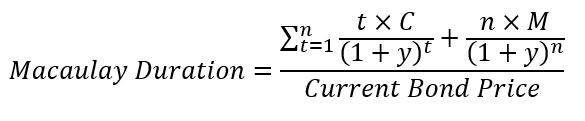
Where:

• t = respective time period
• C = periodic coupon payment
• y = periodic yield
• n = total number of periods
• M = maturity value
• Current Bond Price = present value of cash flows (time value of money).

The DURATION function employs the following syntax to operate:

• settlement: this is required and represents the security's settlement date.  The security settlement date is the date after the issue date when the security is traded to the buyer
• maturity: this is also required.  This is the security's maturity date.  The maturity date is the date when the security expires
• coupon: this is required.  This is the security's annual coupon rate
• yield: again, this is required.  This is the security's annual yield
• frequency: this is required and represents the number of coupon payments per year.  For annual payments, frequency = 1; for semi-annual, frequency = 2; for quarterly, frequency = 4
• basis: this is optional.  The type of day count basis to use.  If this argument is omitted, they will be set to the default value of zero [0].  There are five [5] acceptable values for this argument:
• 0 or omitted: we will use the US (NASD) 30 / 360 day-count convention
• 1: we will use the Actual / actual method which uses the actual number of days in each month and year to calculate the discount rate
• 2: we will use the Actual / 360 method which means that interest or any other relevant accrual factor will be calculated based on the actual number of days elapsed in a year of 360 days
• 3: we will use the Actual / 365 method which means that interest or any other relevant accrual factor will be calculated based on the actual number of days elapsed in a year of 365 days
• 4: we will use the Eurobond 30 / 360 day-count convention.

It should be noted that:

• the dates will be stored as sequential serial numbers so that they can be used in calculations.  30 December 1899 will be day zero [0] in DAX
• there are three [3] different key dates here which we should note here:
• issue: the date the bond or coupon is issued
• settlement: the date a buyer purchases the coupon or bond
• maturity: the date the bond or coupon expires.  For example, there is a 30-year bond issue on 1^st January 2020, and this bond is purchased by a buyer six [6] months later.  Hence, 1^st July 2020 is the settlement date, and the issue date would be 1^st January 2020.  The maturity date should be 1^stJanuary 2050 which is 30 years after the issue date. 
• the settlement and maturity date are shortened to integers
• the frequency and basis are rounded to the nearest integer
• an error is returned if:
• settlement or maturity is not a valid date
• settlement ≥ maturity
• coupon < 0
• yield < 0
• frequency is any number other than 1, 2 or 4
• basis < 0 or basis > 4.
• the DURATION function is not compatible with Power Pivot and currently it is only compatible with Power BI, SSAS Tabular, Azure AS and SSDT
• this function is not supported for use in DirectQuery mode when used in calculated columns or row-level security (RLS) rules.

Consider the following example:

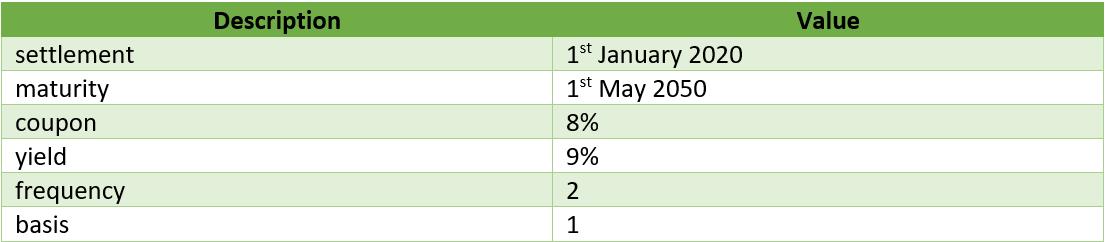
We would enter all these parameters into Power BI as follows:

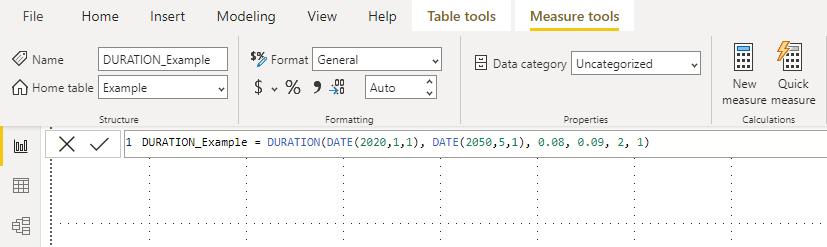
This would return the following figure:

Come back next week for our next post on Power Pivot in the Blog section.  In the meantime, please remember we have training in Power Pivot which you can find out more about here.  If you wish to catch up on past articles in the meantime, you can find all of our Past Power Pivot blogs here.