Power Pivot Principles: The A to Z of DAX Functions – COMBINA
17 May 2022
In our long-established Power Pivot Principles articles, we continue our series on the A to Z of Data Analysis eXpression (DAX) functions. This week, we look at COMBINA.
The COMBINA function

This function returns the number of combinations (with repetitions) for a given number of items. If this sounds a little confusing, think of it this way: you have a number of balls in the bag, each with a different number on it. You take one ball out at random, record its number, then replace it. You do this number_chosen times. Ignoring the sequence of the numbers selected, COMBINA deduces the number of different combinations. Since there is replacement, number_chosen may exceed the number too.
For example, selecting three numbers from a bag of balls numbered 1 to 4 would have the following 20 combinations:
111, 112, 113, 114, 122, 123, 124, 133, 134, 144, 222, 223, 224, 233, 234, 244, 333, 334, 344 and 444.
The COMBINA function employs the following syntax to operate:
COMBINA(number, number_chosen)
The COMBINA function has the following arguments:
- number: this is required and must be greater than or equal to zero. Microsoft states that number must be greater than or equal to number_chosen but this requirement does not seem to hold in practice (see my examples below)
- number_chosen: this is also required and Must be greater than or equal to zero too
- non-integer values for both arguments will be truncated.
It should be further noted that:
- if the value of either argument is outside of its constraints, COMBINA returns the #NUM! error value
- if either argument is a non-numeric value, COMBINA returns the #VALUE! error value
- the following equation is used:
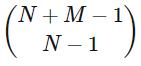
- in the equation above, N is number and M is number_chosen
- this function is not supported for use in DirectQuery mode when used in calculated columns or row-level security (RLS) rules.
Please see my example below:


Here, selecting four numbers from a bag of balls numbered 1 to 3 would have the following 15 combinations:
1111, 1112, 1113, 1122, 1123, 1133, 1222, 1223, 1233, 1333, 2222, 2223, 2233, 2333 and 3333.
Come back next week for our next post on Power Pivot in the Blog section. In the meantime, please remember we have training in Power Pivot which you can find out more about here. If you wish to catch up on past articles in the meantime, you can find all of our Past Power Pivot blogs here.

