Power Pivot Principles: The A to Z of DAX Functions – ATANH
28 September 2021
In our long-established Power Pivot Principles articles, we are starting a new series on the A to Z of Data Analysis eXpression (DAX) functions. This week it’s all a load of hyperbolics…
The ATANH function
Welcome to the wonderful world of “Functions You May Not Use in This or Your Next Life”. Today’s presentation is on the DAX function ATANH, which represents the inverse hyperbolic tangent function. That’s probably as far as I need to go, right...?
If like me, when you were at school you had a life rather than multiple maths lessons, inverse hyperbolic tangent functions may have passed you by. To understand let’s consider the following functions first:
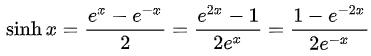
and
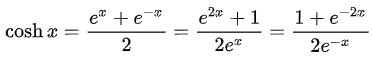
These sorts of functions are used in differential equations and may also be used to derive trigonometric functions with complex arguments, e.g.
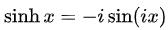
and
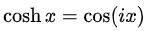
The hyperbolic tangent function is defined (when x does not equal one [1]) as follows:
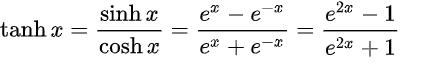
The inverse hyperbolic tangent function, ATANH, is the inverse of tanh x (above), i.e.
ATANH(TANH(number)) = number.
For a given value of a hyperbolic function, the corresponding inverse hyperbolic function provides the corresponding hyperbolic angle. The size of this hyperbolic angle is equal to the area of the corresponding hyperbolic sector of the hyperbola xy = 1, or twice the area of the corresponding sector of the unit hyperbola x2 ? y2 = 1, just as a circular angle is twice the area of the circular sector of the unit circle. Some call the inverse hyperbolic functions "area functions" as a consequence.
The syntax is straightforward:
=ATANH (number)
There is only one argument:
- number: the absolute value of which must not greater than one [1].
Please see my example below:
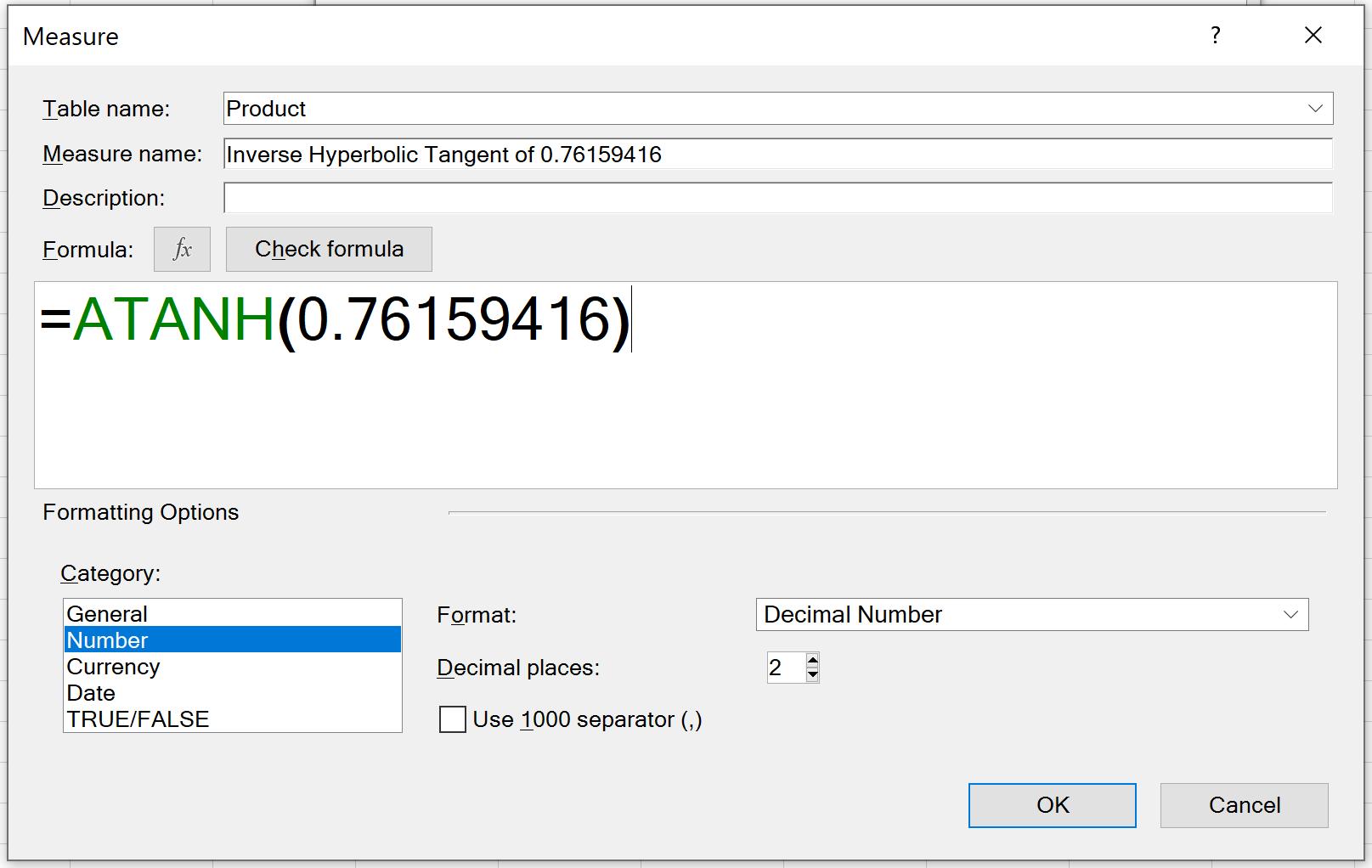

You see? Who would have thought inverse hyperbolic tangents in Data Analysis eXpressions would be so easy!
Come back next week for our next post on Power Pivot in the Blog section. In the meantime, please remember we have training in Power Pivot which you can find out more about here. If you wish to catch up on past articles in the meantime, you can find all of our Past Power Pivot blogs here.

