Power Pivot Principles: The A to Z of DAX Functions – ACCRINT
15 February 2022
In our long-established Power Pivot Principles articles, we continue our series on the A to Z of Data Analysis eXpression (DAX) functions. This week, we look at ACCRINT.
The ACCRINT function
The ACCRINT function returns the accrued interest for a security that pays interest on a periodic basis. It uses the following syntax:
=ACCRINT(issue_date, first_interest_date, settlement_date, rate, par, frequency, [basis], [calculation_method])
Please note both basis and calculation method is optional, which is why they appear in square brackets (don’t add the square brackets!).
The arguments are defined as follows:
- issue_date: this is required and represents the issue date of the security
- first_interest_date: also required; this is the initial date of interest
- settlement_date: again mandatory, this is the date after the issue date when the security is traded to the buyer
- rate: this is required too and is the security’s annual coupon rate (be careful this is entered correctly)
- par: another necessary argument, this is the security’s par value, which is the face value of a share or other security rather than its market value
- frequency: the final required option, this represents number of coupon payments per year. For annual payments, frequency = 1; for semi-annually, frequency = 2; for quarterly, frequency = 4. In other words, calculate based on 12 (number of months in year) divided by the duration (in months) between payments
- basis: this is an optional argument (assumed to be zero [0] if omitted). There are five options:
| Basis | Day count basis |
|---|---|
| 0 or omitted | US (NASD) 30 / 360 |
| 1 | Actual / actual |
| 2 | Actual / 360 |
| 3 | Actual / 365 |
| 4 | European 30 / 360 |
- calculation_method: again optional, this value determines the way to calculate the total accrued interest when the date of settlement is after the first_interest_date. A value of TRUE (1) returns the total accrued interest from issue_date to settlement_date. A value of FALSE (0) returns the accrued interest from first_interest_date to settlement_date. As mentioned, this argument is optional; if not specified, the default value is TRUE.
It should be noted that:
- dates are stored as sequential serial numbers so they can be used in calculations. In DAX, December 30, 1899 is day zero [0], and January 1, 2008 is 39448 because it is 39,448 days after December 30, 1899
- ACCRINT is calculated as follows:
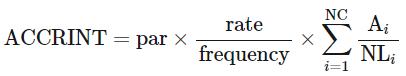
where:
o Ai = number of days for the ith quasi-coupon period within the odd period
o NC = number of quasi-coupon periods that fit in the odd period. If this number contains a fraction, it is raised to the next whole number (i.e. it is rounded up)
o NLi = normal length in days of the quasi-coupon period within the odd period
- issue_date, first_interest_date and settlement_date are truncated to integers
- frequency and basis are rounded to the nearest integer
- an error is returned if:
- issue_date, first_interest_date or settlement_date is / are not (a) valid date(s)
- issue_date ≥ settlement_date
- rate ≤ 0
- par ≤ 0
- frequency is any number other than 1, 2 or 4
- basis < 0 or basis > 4
- this function is not supported for use in DirectQuery mode when used in calculated columns or row-level security (RLS) rules.
Please see my examples below:
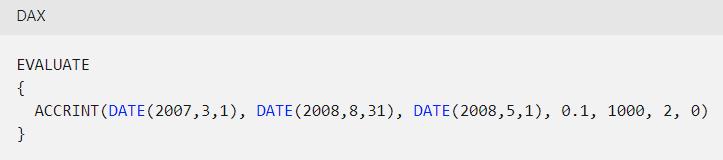
returns the accrued interest of 116.94, from issue_date to settlement_date, for a security with the terms specified above.
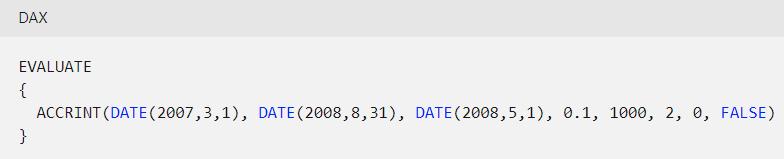
returns the accrued interest of 66.94, from first_interest_date to settlement_date, for a security with the terms specified above.
Come back next week for our next post on Power Pivot in the Blog section. In the meantime, please remember we have training in Power Pivot which you can find out more about here. If you wish to catch up on past articles in the meantime, you can find all of our Past Power Pivot blogs here.

