Monday Morning Mulling: November Challenge
28 November 2016
Final Friday Fix: November Challenge Recap
Sometimes, future results are based on what has happened previously. For instance, creating a sequence which is based on previous values in that sequence, e.g. 10, 9, 8, 7, … This sequence subtracts one from the previous number. Some sequences are surprisingly awkward to forecast. This month’s challenge was one such infamous example…
For the challenge, I had created what is known as a recursive sequence, i.e. a sequence that is based on earlier values in the same sequence. In this instance, the numbers are calculated by adding the previous two numbers together.
The question is: can you write a formula to replace the current calculation in cell I19 that will predict the seventh value (pictured, see cells H19:I19 in the above image), the 15th, the 29th, 107th..?
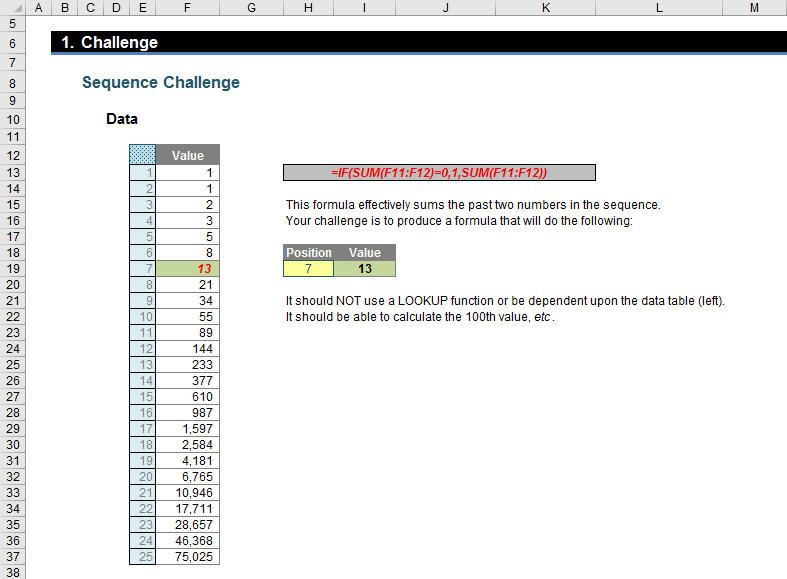
There was just one catch: the formula may not refer to the data table or any extension / variant of it.
This sequence is not only infamous, it’s famous. It’s known as the Fibonacci sequence. Its origins can be traced to a thought experiment about rabbits in the 13th century (really)). Leonardo Pisano Fibonacci posed this question: In an ideal world, how many pairs of rabbits can be produced from a single pair of rabbits over so many years?
If you assume that rabbits reproduce after they are at least one year old and females always produce one pair of rabbits – a male and a female. So, at the end of the first year, we have one pair of rabbits, who are now one year old. By the end of the second year, the female gives birth to a pair of new-born bunnies, which results in a total of two pairs of rabbits. Another a third month passes, the original pair of rabbits produce a pair, and the previous offspring grows to adulthood, leaving a total of three pairs. And so on.
As this continues on and on for each year, the number of pairs is 1, 1, 2, 3, 5, 8,… - that is, the sum of the previous two values in the sequence. It also assumes rabbits live forever!
One way to calculate the Fibonacci series would be to use Binet’s formula:
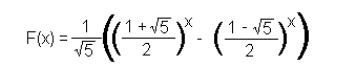
In 1843, Jacques Binet discovered a formula that can also compute the nth term of the Fibonacci series. This is what I used for my solution in the attached Excel file:

There are other ways to calculate the nth term of the Fibonacci series (e.g. Pascal’s triangle). And most don’t do something clever in Excel (e.g. VBA), they do something using mathematics.
Now I must admit I am biased. I am a mathematician. Gentle digits are amongst some of my best friends… One of the first articles I ever wrote was the tongue-firmly-placed-in-cheek little ditty called “Those Who Can Do, Those Who Can’t Use VBA”. The point was not to denigrate programmers (although it was a nice side benefit…), but to emphasise that too often we head straight for a black box solution when there is a simpler, formulaic alternative. Calculating interest on average cash balances is a great example of that (please consider this Thought article for our solution on this age-old pearl of a problem).
No doubt I will be avalanched with simpler solutions – but hey, it works and it is a solution!
For more tricks and tips, check out our many examples at www.sumproduct.com/thought.
The Final Friday Fix will return on Friday 30 December with a new Excel Challenge. In the meantime, please look out for the Daily Excel Tip on our home page and watch out for a new blog every other business workday.

