A to Z of Excel Functions: The NPV Function
13 March 2023
Welcome back to our regular A to Z of Excel Functions blog. Today we look at the NPV function.
The NPV function
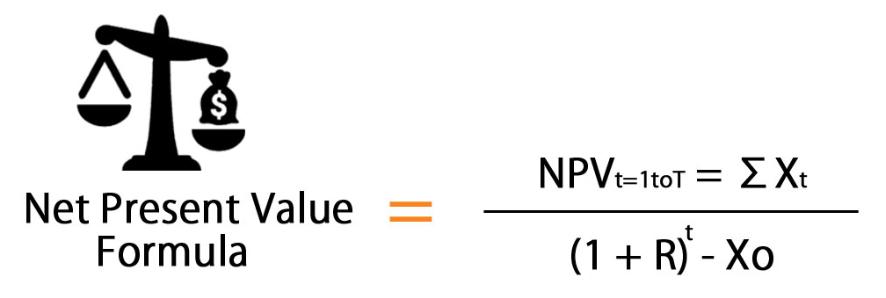
Three-way integrated financial statement modelling may not always be the end game, merely an interim marker. Once you have created your model, you may wish to value it – and there are several ways this may be achieved. One particular approach utilises Discounted Cash Flows and is known as the Net Present Value (NPV) method.
Perhaps the easiest way to think of it is as follows:
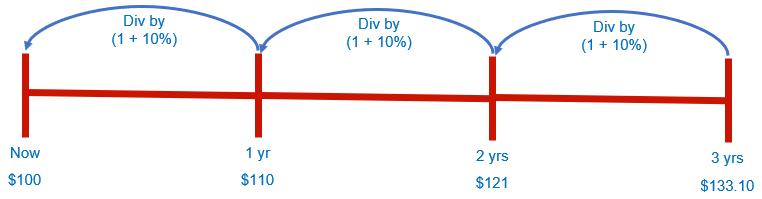
Let’s assume inflation is running at 10% (and we will assume this is after tax as we all earn our wages after tax and increases in spending affect this after-tax wage)
- Something that costs $100 this year will cost 10% more next year, i.e. $110
- Something that costs $110 next year will cost 10% more the year after, i.e. $121
- Something that costs $121 in that year will cost 10% more the following year, i.e. $133.10
- However, they are all worth the equivalent of $100 now (as we “discount” these future values back to their present values).
Valuations include both cash inflows and cash outflows. Adding up all these positive and negative present values, provides a netted off total: the Net Present Value (NPV). The aim is to generate a positive return (a positive NPV) for a given rate of discounting, known as the discount rate.
For example, if the pre-tax cost of debt is 8% and tax is charged at 30%, then the post-tax cost of debt will be 8% x (1 – 30%) = 5.6%. That’s pretty straightforward. We can then calculate the blended rate known as the Weighted Average Cost of Capital (WACC):

Using this discount rate, we must ensure no element in the cash flow includes any reference to financing or the cost of financing, e.g.
- Debt drawdowns or repayments
- Equity issuances or buybacks
- Interest received or paid
- Dividends paid
- Tax shield on interest (i.e. the benefit of the reduced tax due to the interest deduction in the Income Statement).
If any of these elements were to be included, this would effectively constitute a double count, as the discount rate already allows for these factors. When discounting using the WACC discount rate, you are evaluating the value of the cash flows from the perspective of all financial stakeholders. This is known as the Enterprise Value and the cash flow is known as the Free Cash Flow to the Firm (FCFF) or the enterprise cash flow.
If instead you discounted at the cost of equity, this would be for evaluating what a business is worth to the equity stakeholders (i.e. the shareholders). This should in theory equal the market value of the share capital, or Equity Value. The corresponding cash flow here is known as the Free Cash Flow to Equity (FCFE) or the equity cash flow.
Finally, a lesser known fact surrounds discounting at the cost of debt only. This is used for deciding when to lease versus when to buy. Here, the incremental differences in the debt financing cashflows should be reviewed. If you were to assume all debt cashflows as positive (say) and all leasing cashflows as negative, you then evaluate this at the cost of debt (not the rate implicit in the lease). If the NPV is positive, debt flows exceed leasing, so leasing should be chosen, and vice versa.
Enterprise valuations are used for estimating the market value of the business or project; equity value is used for valuing (majority) shareholdings.
Advantages
- Very common approach
- May be used for enterprise and equity valuations
- Often incorporated with probabilistic methods such as simulations analysis.
Disadvantages
- Cash flows used are often calculated incorrectly
- For typical discount rates, the terminal value (i.e. the value derived from cash flows outside of the explicit forecast period) can represent in excess of 80% of the value
- Assumes investors are rational
- Treatment of taxation and interest received is frequently misunderstood.
Assuming you have the appropriate free cash flows, consider the following simple NPV illustration:

Here, I have assumed a multiple period NPV with no terminal value and cash flows all occurring at a point in time (e.g. Time 0, Time 1, …). Stepping out the calculations, clearly the NPV at a discount rate of 8.5% equates to $8,987 in cell H30.
Before I employ the NPV function, let’s consider its syntax:
=NPV(rate, cashflows) or
NPV(rate, value1[, value2,
…])
It should be noted that:
- rate is required. This is the discount rate over the length of one period
- cashflows or value1, value2, ... represent the free cash flows. The argument cashflows or value1 is required, whereas any subsequent values are optional. You may have one [1] to 254 arguments representing these flows
- value1, value2, ... must be equally spaced in time and occur at the end of each period
- NPV uses the order of value1, value2, ... to interpret the order of cash flows
- arguments that are empty cells, logical values or text representations of numbers, error values or text that cannot be translated into numbers are ignored
- if an argument is an array or reference, only numbers in that array or reference are counted. Empty cells, logical values, text or error values in the array or reference are ignored.
NPV is similar to the PV (present value) function. The primary difference between PV and NPV is that PV allows cash flows to begin either at the end or at the beginning of the period. Unlike the variable NPV cash flow values, PV cash flows must be constant throughout the investment.
Furthermore, NPV is also related to the IRR (internal rate of return) function. Given the IRR is the rate for which NPV equals zero, NPV(IRR(cashflows), cashflows) will be zero [0].
If you use the NPV function in the example, you will note that you do not get the same result (see cell H33). This is because the NPV function has one period’s discounting built into it. To correct it, we have two choices:
- multiply the result by (1 + discount_rate)
- exclude the first period (which is undiscounted) and add it to the result afterwards.
The two approaches are shown below for comparison purposes:

This is why we tend to calculate NPVs from first principles and use the NPV or XNPV functions to check our computations instead.
We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.
A full page of the function articles can be found here.

