A to Z of Excel Functions: The MOD Function

Welcome back to our regular A to Z of Excel Functions blog. Today we look at the MOD function.

The MOD function

The MOD function, MOD(number, divisor), returns the remainder after the number (first argument) is divided by the divisor (second argument).  The result has the same sign as the divisor.

For example, 9 / 4 = 2.25, or 2 remainder 1.  MOD(9,4) is an alternative way of expressing this, and hence equals one [1] also.  Note that the 1 may be obtained from the first calculation by (2.25 – 2) x 4 = 1, i.e. in general:

where INT() is the integer function in Excel.

Uses of MOD

This function has various uses and I provide three common examples below:

• Obtaining “residuals”: in some instances in modelling, you need the integer part of a number, e.g. how many payments fall between two dates may calculate as 9.94 – but that’s nonsense.  In this instance, you would have only made nine payments, i.e. INT(9.94).
  
  Similarly, you might want to accrue the fee for payments not yet made.  Using MOD(9.94,1) = 0.94, i.e. the number after the decimal place.  Note that 9.94 – INT(9.94) gives the same result here; the MOD approach is simply shorter
• Calculations at regular time intervals: consider tax payments as an example.  Many companies make tax payments quarterly (i.e. once every three months).  If we assume these payments are made in March, June, September and December then we can formulate the payment as IF(MOD(month_number)=0, make_payment, 0), etc.

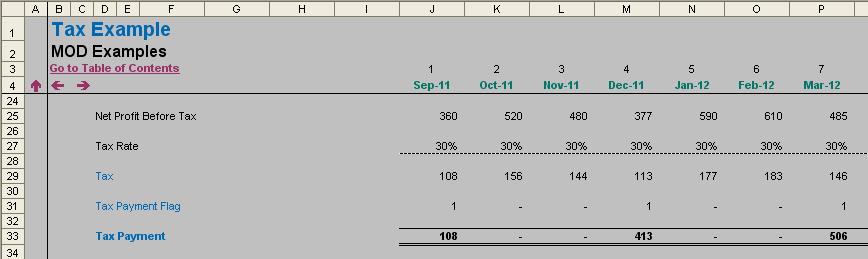
• Summing every nth row: it is not uncommon for users to want to sum every nth cell (e.g. second, third, fourth,…) in a spreadsheet.  Excel has no standard function which will do this, but MOD can come to the rescue.  For example, the array formula

             was used in cell H53 in the following example:

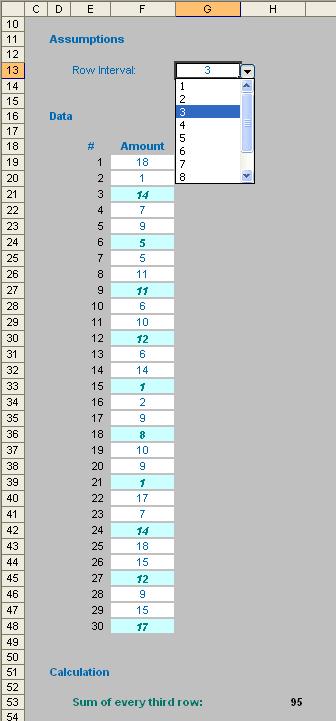
Arrays using large ranges can cause calculations to slow down considerably. This is why I used a counter rather than the volatile ROW() function (volatile functions calculate each time you press ENTER or F9).

Care with MOD (1): Minor Inaccuracies

If accuracy is vital, be careful with MOD as it may give very slightly erroneous results:

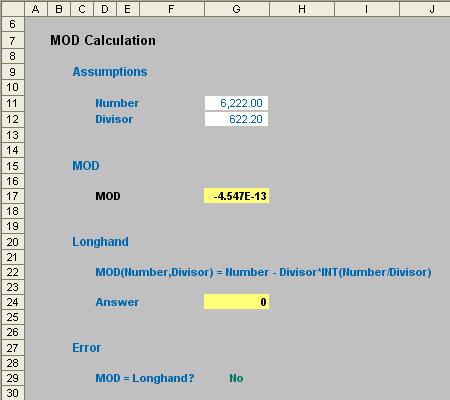
The result for MOD in cell G17 might seem inconsequential, but imagine you were making calculations based on MOD(number, divisor)=0.  In this case, MOD would not equal zero [0] and the calculation would not work.

This issue tends to occur more commonly when working with non-integers. 

The problem here isn’t really MOD.  Calculations are performed in binary [1,0] format and most floating point numbers have no exact binary representation (just as 1/3 has no exact decimal representation).  In this instance, 10 times the binary approximation to 622.2 is

i.e. you may need to use the ROUND(number, number_of_digits) as part of your formula too.

Care with MOD (2): #NUM! Errors

If the number is 134,217,728 (2²⁷) times greater or more than the divisor this gives rise to an #NUM! error, viz.

Some texts suggest that you could use the formula

This will solve for larger numbers much larger than the limit for MOD, but theoretically will hit the same problem when the number being evaluated reaches 134,217,728*134,217,728*divisor.  For most uses, this is limit is large enough that it will never be reached, but I suggest sticking with Microsoft’s recommended solution which is calculating the “longhanded” result as illustrated above (cell G24).

Care with MOD (3): Positives and Negatives

When using the MOD function with one negative number and the expected result is the numerator, MOD(9,-10) returns -1, whereas you could argue the correct result should be 9:

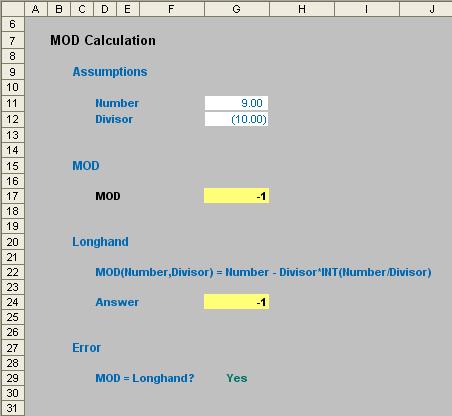
Note that the longhand approach also gives a result of -1.  Microsoft explains that this approach has been taken deliberately in order to be consistent with the dBase MOD function. 

If you always need MOD to deliver a value of x where 0 ? x < divisor, then use the adjusted formula:

And Finally…

In summary, I suppose you can say that MOD does cause division amongst financial modellers!

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.

A full page of the function articles can be found here.