A to Z of Excel Functions: The MINVERSE Function

Welcome back to our regular A to Z of Excel Functions blog. Today we look at the MINVERSE function.

The MINVERSE function

In mathematics, especially in areas such as linear algebra, matrices may be used to solve simultaneous equations. For the record, a matrix is not just a movie it’s a rectangular arrangement of m x n elements, in the dimensions of m rows by n columns, e.g. a matrix A (say) may be represented as

It is often written in compact form as

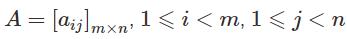
An n x n square matrix A is called invertible (also non-singular or non-degenerate), if there exists an n x n square matrix B such that

where I_n denotes the n x n identity matrix and the multiplication used is ordinary matrix multiplication.  If this is the case, then the matrix B is uniquely determined by A, and is called the (multiplicative) inverse of A, denoted by A^?1.  Matrix inversion is the process of finding the matrix B that satisfies the prior equation for a given invertible matrix A.

A square matrix that is not invertible is called singular or degenerate.  A square matrix is singular if and only if its determinant is zero.  Singular matrices are rare in the sense that if a square matrix's entries are randomly selected from any finite region on the number line or complex plane, the probability that the matrix is singular is zero [0], that is, it will "almost never" be singular.  Non-square matrices (m x n matrices for which m ? n) do not have an inverse.  However, in some cases such a matrix may have a left inverse or right inverse.  If A is m x n and the rank of A is equal to n (n ? m), then A has a left inverse, an n x m matrix B such that BA = I_n.  If A has rank m (m ? n), then it has a right inverse, an n x m matrix B such that AB = I_m.

The Excel function MINVERSE returns the inverse matrix for a matrix stored in an array.  It has the following syntax:

where:

• array is required, and represents a numerical array with an equal number of rows and columns.

It should be noted that:

• array may be given as:
  • a cell range, e.g. A1:C3
  • an array constant, such as {1,2,3;4,5,6;7,8,9}
  • a name to either of these
• MINVERSE returns the #VALUE! error when:
  • any cells in array are empty or contain text
  • array does not have an equal number of rows and columns
• matrix determinants are generally used for solving systems of mathematical equations that involve several variables
  
• MINVERSE is calculated with an accuracy of approximately 16 digits, which may lead to a small numeric error when the calculation is not complete.  For example, the determinant of a singular matrix may differ from zero by 1E-16
  
• some square matrices cannot be inverted and will return the #NUM! error value with MINVERSE.  The determinant for a non-invertible matrix is zero [0].

If you have a current version of Microsoft 365, then you can simply enter the formula in the top-left-cell of the output range, then press ENTER to confirm the formula as a dynamic array formula.  Otherwise, the formula must be entered as a legacy array formula by first selecting the output range, entering the formula in the top-left-cell of the output range, and then pressing CTRL + SHIFT + ENTER to confirm it.  Excel inserts curly brackets (“braces”) at the beginning and end of the formula.

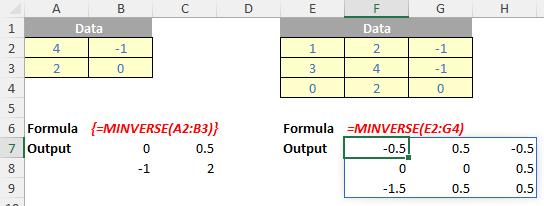
As an example:

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.

A full page of the function articles can be found here.