A to Z of Excel Functions: The MDURATION Function
14 February 2022
Welcome back to our regular A to Z of Excel Functions blog. Today we look at the MDURATION function.
The MDURATION function
Not to be confused with PDURATION, this function returns the modified Macauley duration for a security with an assumed par value of $100.
Whereas the modified duration measures the price sensitivity of a bond when there is a change in the yield to maturity, the (modified) Macauley duration calculates the weighted average time before a bondholder would receive the security’s cash flows. It is frequently used by portfolio managers who wish to adopt what is known as an immunization strategy (nothing to do with COVID-19).
The Macaulay duration is calculated by multiplying the time period by the periodic coupon payment and dividing the resulting value by 1 plus the periodic yield raised to the time to maturity. Next, the value is calculated for each period and added together. Then, the resulting value is added to the total number of periods multiplied by the par value, divided by 1, plus the periodic yield raised to the total number of periods. This is then divided by the current bond price.

As stated above, the MDURATION function returns this modified Macauley duration for a security with an assumed par value of $100. It employs the following syntax to operate:
MDURATION(settlement, maturity, coupon, yield, frequency, [basis])
The MDURATION function has the following arguments:
- settlement: this is required and represents the security's settlement date. The security settlement date is the date after the issue date when the security is traded to the buyer
- maturity: this is also required, and is the security's maturity date, i.e. when the security expires
- coupon: again required, this is the security’s annual coupon rate
- yield: another required argument, this is the security’s annual yield
- frequency: another mandatory field, this is the number of coupon payments per year. For annual payments, frequency is 1; for semiannual, frequency is 2; for quarterly, frequency is 4. These are the only options (see below)
- basis: the type of day count basis to use. This is optional. There are five options:
| Basis | Day count basis |
|---|---|
| 0 or omitted | US (NASD) 30 / 360 |
| 1 | Actual / actual |
| 2 | Actual / 360 |
| 3 | Actual / 365 |
| 4 | European 30 / 360 |
It should be further noted that:
- Microsoft Excel stores dates as sequential serial numbers so they can be used in calculations. By default, January 1, 1900 is serial number 1, and January 1, 2008 is serial number 39448 because it is 39,448 days after January 1, 1900
- dates should be entered using the DATE function, or as results of other formulae or functions. For example, use =DATE(2020,2,29) for the 29th of February 2020. Problems may occur if dates are entered as text
- the settlement date is the date a buyer purchases a coupon, such as a bond. The maturity date is the date when a coupon expires. For example, suppose a 30-year bond is issued on January 1, 2008, and is purchased by a buyer six months later. The issue date would be January 1, 2008, the settlement date would be July 1, 2008, and the maturity date would be January 1, 2038, 30 years after the January 1, 2008, issue date
- the arguments settlement, maturity, frequency and basis are truncated to integers
- if settlement or maturity is not a valid date, MDURATION returns the #VALUE! error value
- if yield is less than zero [0], MDURATION returns the #NUM! error value
- if frequency is any number other than 1, 2, or 4, MDURATION returns the #NUM! error value
- if basis < 0 or if basis > 4, MDURATION returns the #NUM! error value
- if settlement ≥ maturity, MDURATION returns the #NUM! error value
- Excel calculates MDURATION as follows:
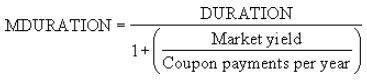
Please see my example below:
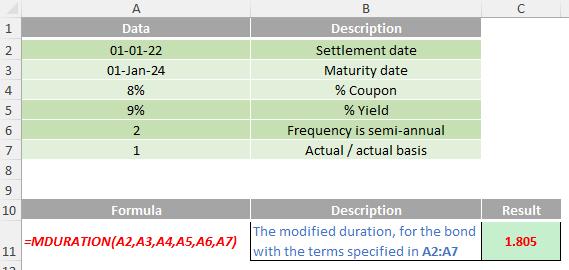
We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.
A full page of the function articles can be found here.

