A to Z of Excel Functions: The MAX Function
10 January 2022
Welcome back to our regular A to Z of Excel Functions blog. Today we look at the MAX function.
The MAX function
MAX (and MIN) may be familiar to many Excel users, but it is still probably worth performing a recap. MAX does exactly what it says on the tin – it calculates the maximum value in a range:

Modellers frequently make mistakes with MAX:

These examples highlight that you should be careful with using blanks both in the ranges and in the formulae themselves. Regular readers will notice I often omit zeros in my formulae but with MAX (and MIN) I will often take care to explicitly use zeros.
The MAX function has the following syntax:
MAX(number1, [number2, …])
The MAX function has the following argument(s):
- number1, number2, …: number1 is required, but subsequent numbers are optional
- you may have up to 255 arguments in order to find the maximum value.
It should be noted that:
- arguments may be numbers, or names, arrays or references that contain numbers
- logical values and text representations of numbers that you type directly into the list of arguments are counted
- if an argument is an array or reference, only numbers in that array or reference are used; empty cells, logical values or text in the array or reference are ignored
- if the arguments contain no numbers, MAX returns zero (0)
- arguments that are error values or text that cannot be translated into numbers cause errors
- if you want to include logical values and text representations of numbers in a reference as part of the calculation, use the MAXA function instead.
There is a highly relevant finance example combining MAX and MIN functions (MIN is the similar function that returns the minimum value in a range), namely calculating the maximum dividend allowable for a particular period.
Dividends may only be paid out of what are known as distributable reserves (this is a bit of an oxymoron as dividends are also known as distributions). Revaluation reserves, share premium accounts, capital redemption reserves are all non-distributable. Essentially, dividends may only be paid out of the current year’s Net Profit After Tax (NPAT) and the aggregation of all previous year’s profits after past distributions, Retained Earnings. Dividends may not make the Balance Sheet’s Total Equity become negative. This shows insolvency and this sort of distribution is illegal in most territories. Given non-distributable reserves may not become negative allow me to concentrate simply on NPAT and Retained Earnings here.
To derive the maximum dividend allowable, let me consider some scenarios. Let’s imagine the following scenario:

It isn’t rocket science that if Retained Earnings and NPAT are both positive, then the maximum dividend allowed is the sum of the two.

If NPAT is negative, but Retained Earnings are positive and exceed the NPAT figure, then the maximum dividend allowed is the net of the two figures. Should the net be negative, no dividend is allowed.

Here is the one that often surprises people. If Retained Earnings is negative but NPAT is positive, regardless of whether the net is positive or negative, the maximum dividend allowed is the NPAT amount. This may seem incomprehensible upon first thought, but it is typically dependent upon two conditions:
- The company’s auditors must sign off on it. This is to ensure the company is still seen to be a going concern (i.e. it can still continue to operate and trade its way out of any short-term difficulties).
- The shareholders must vote for it. Almost as hilarious as when Members of Parliament solemnly vote for their 50% pay rise each year.
If you think about it some more, this makes sense. Remember, dividends cannot be paid if the company is insolvent. The auditors check to see whether the company can “afford” it for other reasons. But if you don’t allow this scenario how would anyone ever attract share capital for a start-up company? A new company may have to provide for certain factors which may never come to fruition. A large non-current asset may have to be written off as not fit for purpose if a company’s strategy changes without any cash consequence. Is it acceptable that shareholders have to wait 10 years for the Retained Earnings losses to be covered even if the business is hugely profitable in the meantime? No, and this is precisely why this is the rule in many territories.
The next scenario is more obvious:

With both a negative NPAT and Retained Earnings, there is no leeway now. These scenarios seem to suggest the following formula:
=MAX(NPAT + Retained Earnings, NPAT, 0)
This allows for the above scenarios. The check to ensure that the value is non-negative (i.e. the inclusion of zero in the MAX formula) is so that shareholders do not get asked to pay a dividend to the company. I can’t imagine that would go down too well.
We are not done yet though. Let’s go back to the penultimate scenario but now consider the cash position as well:

Here, the Cash Available is the total amount of cash available to pay the dividend. Technically, this includes any cash reserves built up over time, but many companies only consider the cash position for the period the dividend relates to (this is the scenario I shall be modelling in the case study shortly). This seems to suggest the formula:
=MIN(MAX(NPAT + Retained Earnings, NPAT, 0), Cash Available)
Let me just check with slightly revised numbers:

In this scenario, the company is overdrawn. Oops. Here, this company is going to be asking for money again from its shareholders. Not a good idea. This leads to the slightly revised – and finally correct – formula:
Maximum Dividend = MAX(MIN(MAX(NPAT + Retained Earnings, NPAT), Cash Available), 0)
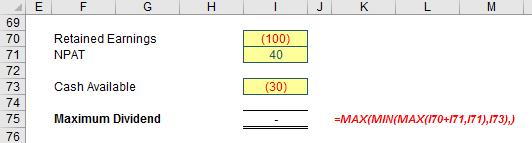
Ah yes, the wonderful MAX(MIN(MAX)) formula. It may not be the prettiest formula in the world, but the point is, it gives the right number.
We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.
A full page of the function articles can be found here.

