A to Z of Excel Functions: The IMSUM Function

Welcome back to our regular A to Z of Excel Functions blog. Today we look at the IMSUM function.

The IMSUM function

An imaginary number is a complex number that can be written as a real number multiplied by the imaginary unit i (sometimes denoted j) which is defined by its property i² = −1.  In general, the square of an imaginary number bi is −b².  For example, 9i is an imaginary number, and its square is −81.  Zero is considered to be both real and imaginary.

An imaginary number bi can be added to a real number a to form a complex number of the form a + bi, where the real numbers a and b are called, respectively, the real part and the imaginary part of the complex number.

Sometimes you might wish to add one complex number to one or more other complex numbers.  IMSUM returns the sum of two or more complex numbers in the x + yi or x + yj text format. 

The IMSUM function employs the following syntax to operate:

The IMSUM function has the following arguments:

• inumber1, [inumber2], …: inumber1 is required; other arguments are optional.  Between 1 and 255 complex numbers may be added together.

It should be further noted that:

• you should use COMPLEX to convert real and imaginary coefficients into a complex number
• IMSUM recognises either the i or j notation
• if any of inumber1, [inumber2], … is a value that is not in the x + yi or x + yj text format, IMSUM returns the #NUM! error value
• if any of inumber1, [inumber2], … is a logical value, IMSUM returns the #VALUE! error value
• if any of inumber1, [inumber2], … is non-numeric, IMSUM returns the #VALUE! error value
• if any complex number ends in +i or -i (or j), i.e. there is no coefficient between the operator and the imaginary unit, there must be no space, otherwise IMSUM will return an #NUM! error
• the addition of two complex numbers is given by:

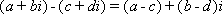
Please see my example below:

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.

A full page of the function articles can be found here.