A to Z of Excel Functions: The IMCSCH Function
7 September 2020
Welcome back to our regular A to Z of Excel Functions blog. Today we look at the IMCSCH function.
The IMCSCH function
An imaginary number is a complex number that can be written as a real number multiplied by the imaginary unit i (sometimes denoted j) which is defined by its property i2 = −1. In general, the square of an imaginary number bi is −b2. For example, 9i is an imaginary number, and its square is −81. Zero is considered to be both real and imaginary.
An imaginary number bi can be added to a real number a to form a complex number of the form a + bi, where the real numbers a and b are called, respectively, the real part and the imaginary part of the complex number.
The polar form of a complex number is another way to represent the number. The form z = a + bi is called the rectangular form of a complex number.
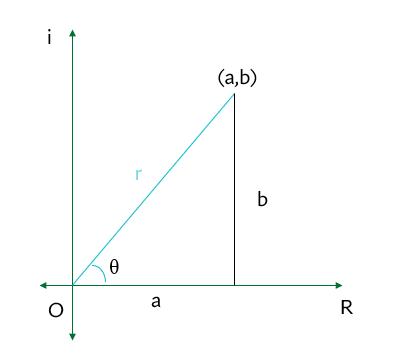
The horizontal axis is the real axis and the vertical axis is the imaginary axis. You can find the real and imaginary components in terms of r and θ, where r is the length of the vector and θ is the angle made with the real axis.
From the Pythagorean Theorem,
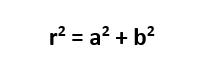
By using the basic trigonometric ratios,

Therefore, multiplying each side by r:

Therefore,
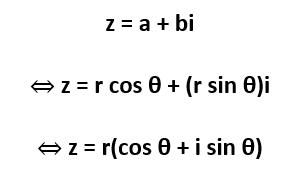
In the case of a complex number, r represents the absolute value, or modulus (where:
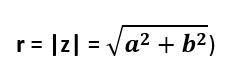
and the angle θ is called the argument of the complex number,
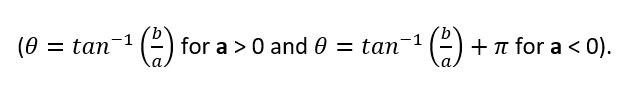
The hyperbolic cosecant (the reciprocal of the hyperbolic sine function) is defined by the following relationships:
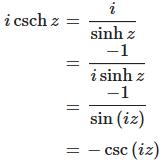
The IMCSCH function returns the hyperbolic cosecant of a complex number in x + yi or x + yj text format.
The IMCSCH function employs the following syntax to operate:
IMCSCH(inumber)
The IMCSCH function has the following argument:
- inumber: this is required and represents the complex number for which you want to calculate the hyperbolic cosecant.
It should be further noted that:
- you should use >COMPLEX to convert real and imaginary coefficients into a complex number
- IMCSCH recognises either the i or j notation
- if inumber is a value that is not in the x + yi or x + yj text format, IMCSCH returns the #NUM! error value
- if inumber is a logical value, IMCSCH returns the #VALUE! error value
- if the complex number ends in +i or -i (or j), i.e. there is no coefficient between the operator and the imaginary unit, there must be no space, otherwise IMCSCH will return an #NUM! error.
Please see my example below:

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.
A full page of the function articles can be found here.

