A to Z of Excel Functions: The IMCOT Function
17 August 2020
Welcome back to our regular A to Z of Excel Functions blog. Today we look at the IMCOT function.
The IMCOT function
An imaginary number is a complex number that can be written as a real number multiplied by the imaginary unit i (sometimes denoted j) which is defined by its property i2 = −1. In general, the square of an imaginary number bi is −b2. For example, 9i is an imaginary number, and its square is −81. Zero is considered to be both real and imaginary.
An imaginary number bi can be added to a real number a to form a complex number of the form a + bi, where the real numbers a and b are called, respectively, the real part and the imaginary part of the complex number.
The polar form of a complex number is another way to represent the number. The form z = a + bi is called the rectangular form of a complex number.

The horizontal axis is the real axis and the vertical axis is the imaginary axis. You can find the real and imaginary components in terms of r and θ, where r is the length of the vector and θ is the angle made with the real axis.
From the Pythagorean Theorem,
r2 = a2 + b2
By using the basic trigonometric ratios,
cos θ = a / r and sin θ = b / r
Therefore, multiplying each side by r:
r cos θ = a and r sin θ = b
Therefore,
z = a + bi
z = r cos θ + (r sin θ)i
z = r(cos θ + i sin θ)
In the case of a complex number, r represents the absolute value, or modulus (where r = |z| = √(a2+b2)), and the angle θ is called the argument of the complex number (θ = tan-1(b/a) for a > 0 and θ = tan-1(b/a) + π for a < 0).
Since the cotangent is the reciprocal of the tangent, the cotangent is equal to the adjacent side divided by the length of the opposite side for θ. Ignoring all the required hefty mathematics,
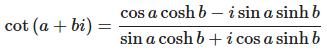
The IMCOT function returns the cotangent of a complex number in x + yi or x + yj text format.
The IMCOT function employs the following syntax to operate:
IMCOT(inumber)
The IMCOT function has the following argument:
- inumber: this is required and represents the complex number for which you want to calculate the cotangent.
It should be further noted that:
- you should use >COMPLEX to convert real and imaginary coefficients into a complex number
- IMCOT recognises either the i or j notation
- if inumber is a value that is not in the x + yi or x + yj text format, IMCOT returns the #NUM! error value
- if inumber is a logical value, IMCOT returns the #VALUE! error value
- if the complex number ends in +i or -i (or j), i.e. there is no coefficient between the operator and the imaginary unit, there must be no space, otherwise IMCOT will return an #NUM! error.
Please see my example below:

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.
A full page of the function articles can be found here.

