A to Z of Excel Functions: The IMABS Function

Welcome back to our regular A to Z of Excel Functions blog. Today we look at the IMABS function.

The IMABS function

An imaginary number is a complex number that can be written as a real number multiplied by the imaginary unit i (sometimes denoted j) which is defined by its property i² = −1.  In general, the square of an imaginary number bi is −b².  For example, 9i is an imaginary number, and its square is −81.  Zero is considered to be both real and imaginary.

An imaginary number bi can be added to a real number a to form a complex number of the form a + bi, where the real numbers a and b are called, respectively, the real part and the imaginary part of the complex number.

Just like the Excel function ABS measures the “distance” between a number and zero (0) (e.g. ABS(-5) is five (5) units from zero (0), therefore, ABS(-5) = 5), so IMABS(“a + bi”) measures the distance from zero (0) to the point z = a + bi.  As can be clearly seen in the diagram, this distance is given by Pythagoras’ Theorem

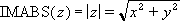
Technically, IMABS returns the absolute value, or modulus, of a complex number a + bi, provided the number has been provided in said text format.

The IMABS function employs the following syntax to operate:

The IMABS function has the following argument:

• inumber: this is required and represents the complex number for which you want the absolute value.

It should be further noted that:

• you should use COMPLEX to convert real and imaginary coefficients into a complex number
• IMABS recognises either the i or j notation
• if the complex number ends in +i or -i (or j), i.e. there is no coefficient between the operator and the imaginary unit, there must be no space, otherwise IMABS will return an #NUM! error.

Please see my example below: 

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.

A full page of the function articles can be found here.