A to Z of Excel Functions: The HYPGEOM.DIST Function

Welcome back to our regular A to Z of Excel Functions blog. Today we look at the HYPGEOM.DIST function.

The HYPGEOM.DIST function

The hypergeometric distribution is used to calculate probabilities when sampling without replacement.  For example, suppose you first randomly sample one card from a deck of 52.  Then, without putting the card back in the deck you sample a second and then (again without replacing cards) a third.  Given this sampling procedure, what is the probability that exactly two of the sampled cards will be aces (four of the 52 cards in the deck are aces).  You can calculate this probability using the following formula based on the hypergeometric distribution:

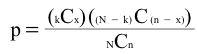
where:

• k is the number of successes in the population
• x is the number of successes in the sample
• N is the size of the population
• n is the number sampled
• p is the probability of obtaining exactly x successes
• _kC_x is the number of combinations of k things taken x at a time.

In this example, k = 4 because there are four aces in the deck, x = 2 because the problem asks about the probability of getting two aces, N = 52 because there are 52 cards in a deck, and n = 3 because 3 cards were sampled. Therefore,

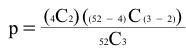
which equates to:

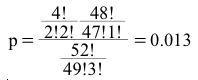
The mean and standard deviation of the hypergeometric distribution are given by:

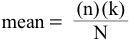
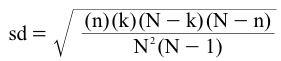
Note that it would not be a binomial experiment. A binomial experiment requires that the probability of success be constant on every trial. With the above experiment, the probability of a success changes on every trial. In the beginning, the probability of selecting an ace is 4/52 (=1/13). If you select an ace on the first trial, the probability of selecting an ace on the second trial is 3/51 (=1/17). If you don’t select am ace on the first trial, the probability of selecting an ace on the second trial is 4/51.

Note further that if you selected the cards with replacement, the probability of success would not change. It would be 1/13 on every trial. Then, this would be a binomial experiment.

The HYPGEOM.DIST function returns the hypergeometric distribution. HYPGEOM.DIST returns the probability of a given number of sample successes, given the sample size, population successes and population size. You should use HYPGEOM.DIST for problems with a finite population, where each observation is either a success or a failure, and where each subset of a given size is chosen with equal likelihood.

It has the following syntax:

HYPGEOM.DIST(sample_s, number_sample, population_s, number_population, cumulative)

The HYPGEOM.DIST function has the following arguments:

• sample_s: this is required and represents the number of successes in the sample
• number_sample: this is also required. This is the size of the sample
• population_s: again, this is required. This reflects the number of successes in the population
• number_population: this is required, and is the population size
• cumulative: this final argument is also required. This is a logical value that determines the form of the function. If cumulative is TRUE, then HYPGEOM.DIST returns the cumulative distribution function; if FALSE, it returns the probability mass function.

It should be further noted that:

• this function is a more versatile form of HYPGEOMDIST, which was available in older versions of Excel
• all arguments are truncated to integers
• if any argument is nonnumeric, HYPGEOM.DIST returns the #VALUE! error value
• if sample_s < 0 or sample_s is greater than the lesser of number_sample or population_s, HYPGEOM.DIST returns the #NUM! error value
• if sample_s is less than the larger of zero (0) or (number_sample - number_population + population_s), HYPGEOM.DIST returns the #NUM! error value
• if number_sample ? 0 or number_sample > number_population, HYPGEOM.DIST returns the #NUM! error value
• if population_s ? 0 or population_s > number_population, HYPGEOM.DIST returns the #NUM! error value
• if number_population ? 0, HYPGEOM.DIST returns the #NUM! error value

as stated above, the equation for the hypergeometric distribution is:

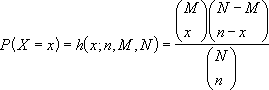
where:

• x = sample_s
• n = number_sample
• M = population_s
• N = number_population.

HYPGEOM.DIST is used in sampling without replacement from a finite population.

Please see my example below:

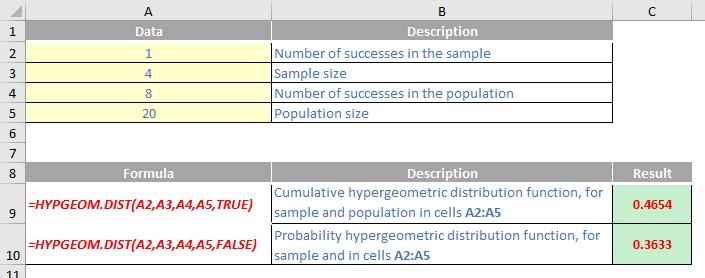
We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.

A full page of the function articles can be found here.