A to Z of Excel Functions: The HARMEAN Function

Welcome back to our regular A to Z of Excel Functions blog. Today we look at the HARMEAN function.

The HARMEAN function

A dangerous function for Ean, they say a picture tells a thousand words:

This time, I think this is true, provided the words are in Swahili (apologies to both of our Swahili readers).

In mathematics, there are three averages known as the three classical Pythagorean means are the arithmetic mean (AM), the geometric mean (GM), and the harmonic mean (HM). These means were studied with proportions by Pythagoreans and later generations of mathematicians because of their importance in geometry and music. Face it, if you work in Excel, you’re a budding mathematician!

They are defined by:

Each mean, M, has the following properties:

• Value preservation

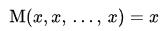
• Scalar consistency – also known as first order homogeneity

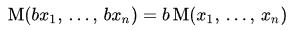
• Invariance under exchange (i.e. you may swap the values without effect)

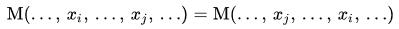
• Averaging

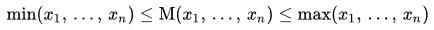
The harmonic and arithmetic means are reciprocal duals of each other for positive arguments:

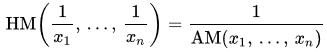
whereas the geometric mean is its own reciprocal dual:

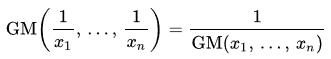
There is an ordering to these means (if all of the x_iare positive)

with equality holding if and only if the x_i are all equal.

Returning to our graphic,

this is a geometric construction of various means of a and b:

• the arithmetic average A (>AVERAGE)
• the geometric mean G (GEOMEAN)
• the harmonic mean H (HARMEAN)
• the quadratic mean Q (also known as the root mean square, which is not a Pythagorean mean, but is “simply” the square root of the arithmetic mean of the squares of a set of numbers). It has no Excel function, but can be calculated using basic operators and functions in Excel.

With understanding, it provides a graphical illustration of the relationship between these four means.

The harmonic mean (also known as the subcontrary mean) is often used to calculate average rates, for example. It is simple to calculate:

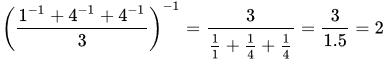
The HARMEAN function has the following syntax:

It has the following argument(s):

• number1, number2, ...: only number1 is required, subsequent numbers are optional.  You may have between one (1) and 255 arguments to calculate the mean
• you may also use a single array or a reference to an array instead of arguments separated by commas.

It should also be noted that:

• as stated above, the harmonic mean is always less than the geometric mean, which is always less than the arithmetic mean
• arguments can either be numbers or names, arrays or references that contain numbers
• logical values and text representations of numbers that you type directly into the list of arguments are counted
• if an array or reference argument contains text, logical values or empty cells, those values are ignored; however, cells with the value zero (0) are included
• arguments that are error values or text that cannot be translated into numbers cause errors
• if any data point ? 0, HARMEAN returns the #NUM! error value.

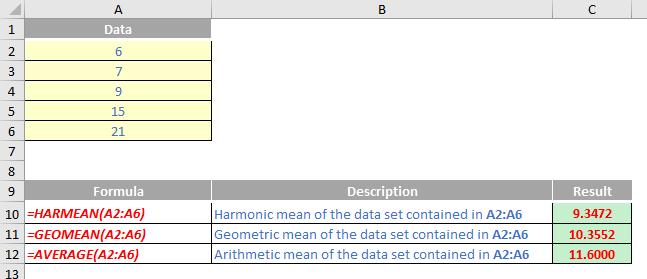
Please see my example below: 

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.

A full page of the function articles can be found here.