A to Z of Excel Functions: The GAMMA Function

Welcome back to our regular A to Z of Excel Functions blog.  Today we look at the GAMMA function.

The GAMMA function

The Gamma distribution is widely used in engineering, science and business, to model continuous variables that are always positive and have skewed distributions.  The Gamma distribution can be useful for any variable which is always positive, such as cohesion or shear strength for example. 

It is a distribution that arises naturally in processes for which the waiting times between events are relevant, and is often thought of as a waiting time between Poisson distributed events (the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval).

To understand it, first think of factorials, e.g. 5! = 5 x 4 x 3 x 2 x 1 = 120.  So far, so good, but how do you calculate if the factorial number you want to evaluate isn’t an integer?  The Gamma function is used to calculate this:

That’s great (if a little recursive), so can be expressed better (!) mathematically as follows:

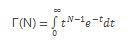
Clear as mud? Well, it gets better. The Gamma distribution just referred to has the following probability density function:

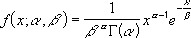
where Г(α) is the Gamma function, and the parameters α and β are both positive, i.e. α > 0 and β > 0:

• α is known as the shape parameter, while β is referred to as the scale parameter
• β has the effect of stretching or compressing the range of the Gamma distribution.  A Gamma distribution with β = 1 is known as the standard Gamma distribution.

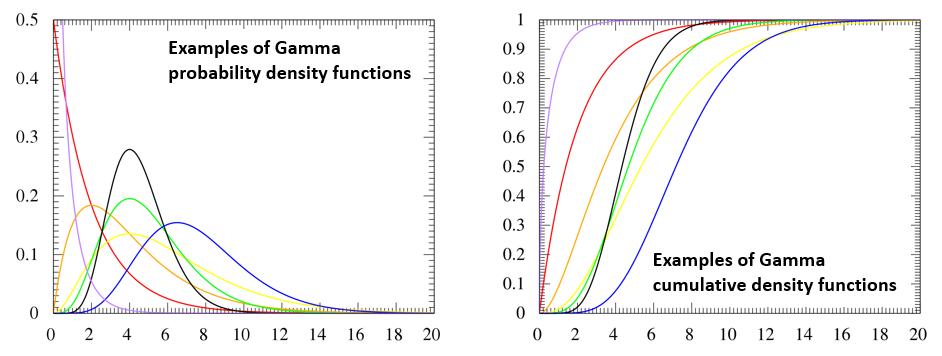
The Gamma distribution represents a family of shapes.  As suggested by its name, α controls the shape of the family of distributions.  The fundamental shapes are characterized by the following values of α:

• Case I (α < 1): when α < 1, the Gamma distribution is exponentially shaped and asymptotic to both the vertical and horizontal axes
• Case II (α = 1): the Gamma distribution with shape parameter α = 1 and scale parameter β is the same as an exponential distribution of scale parameter (or mean) β
• Case III (α > 1): when α is greater than one, the Gamma distribution assumes a mounded (unimodal), but skewed shape.  The skewness reduces as the value of α increases.

The GAMMA function here calculates the above function, Г(N), when β equals one (1):  

The GAMMA function has the following argument:

• number: this is required and represents the number to be evaluated.

It should be noted that:

• if number is either negative integer or zero (0), GAMMA returns the #NUM! error value (arguably, if it is zero, the value should actually be zero!)
• if number contains characters that are not valid, GAMMA returns the #VALUE! error value.

Please see my example below: 

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.

A full page of the function articles can be found here.