A to Z of Excel Functions: The FORECAST.ETS.SEASONALITY Function

Welcome back to our regular A to Z of Excel Functions blog. Today we look at the FORECAST.ETS.SEASONALITY function.

The FORECAST.ETS.SEASONALITY function

A window function (also known as an apodization or tapering function) is a mathematical function that has a zero value outside of a chosen interval. Uniform distributions and the bell curve are two such window functions commonly used in statistics.

Exponential smoothing is what’s known as a rule of thumb technique (i.e. not strictly accurate) for smoothing time series data using the exponential window function. The aim is to smooth out historical data to predict trends, etc.

The aim is to develop a technique to identify what would be next in a series, i.e. forecast the future.  There are various approaches used:

• Naïve method: this really does live up to its billing – you simply use the last number in the sequence, e.g. the continuation of the series 8, 17, 13, 15, 19, 14, … would be 14, 14, 14, 14, …  Hmm, great
  
• Simple average: only a slightly better idea: here, you use the average of the historical series, e.g. for the continuation of the series 8, 17, 13, 15, 19, 14, … would be 14.3, 14.3, 14.3, 14.3, …  
  
• Moving average: now we start to look at smoothing out the trends by taking the average of the last n items.  For example, if n were 3, then the sequence continuation of 8, 17, 13, 15, 19, 14, … would be 16, 16.3, 15.4, 15.9, 15.9, …
• Weighted moving average: the criticism of the moving average is that older periods carry as much weighting as more recent periods, which is often not the case.  Therefore, a weighted moving average is a moving average where within the sliding window values are given different weights, typically so that more recent points matter more.  For example, instead of selecting a window size, it requires a list of weights (which should add up to 1).  As an illustration, if we picked four periods and [0.1, 0.2, 0.3, 0.4] as weights, we would be giving 10%, 20%, 30% and 40% to the last 4 points respectively which would add up to 1 (which is what it would need to do to compute the average).
  Therefore the continuation of the series 8, 17, 13, 15, 19, 14, … would be 15.6, 15.7, 15.7, 15.5, 15.6, …

• Single exponential smoothing: imagine a weighted average where we consider all of the data points, while assigning exponentially smaller weights as we go back in time. For example, if we started with 0.9, our weights would be (going back in time): 0.9, 0.9², 0.9³, 0.9⁴, 0.9⁵, … eventually tending to zero. 
  There is a problem here though: the weights do not add up to 1.  The sum of the first three numbers alone is already 2.439.  This method needs to be modified using the following succinct and elegant formula:

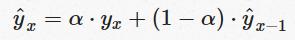
• This is the sum of two products: α.y_x and (1−α)⋅y^{^}_x.  You can think of α (alpha) as a sort of a starting weight 0.9 in the above example.  It is called the smoothing factor or smoothing coefficient.  Given essentially we have a weighted moving average with two weights: α and 1−α, the sum of these is 1, so all is acceptable for calculation purposes.
  
  This gives rise to a recursive technique – hence why this method is called exponential
• Double exponential smoothing: all of the methods above are only good for predicting a single point.  Double exponential smoothing the y-intercept and the gradient of two points from a sample, viz.

The y-intercept is often known as the level and the gradient is known as the trend. The trend may be additive (add 10,000 each period) or multiplicative (increase by 10% each period). It is shown in statistics that a ratio (i.e. the multiplicative approach) is a more stable predictor.

Double exponential smoothing then is nothing more than exponential smoothing applied to both level and trend. To express this in mathematical notation we now need three equations: one for level, one for the trend and one to combine the level and trend to get the expected y.

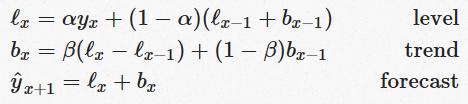
• Exponential Triple Smoothing (ETS): this approach takes it to the next level – how to forecast for many points. This means we need to consider seasonality too: that a series may be repetitive at regular intervals with s seasonal components and length L.
  The idea behind triple exponential smoothing is to apply exponential smoothing to the seasonal components in addition to level and trend. The smoothing is applied across seasons, e.g. the seasonal component of the third point into the season would be exponentially smoothed with the one from the third point of last season, third point two seasons ago, etc. This, we now have four equations:

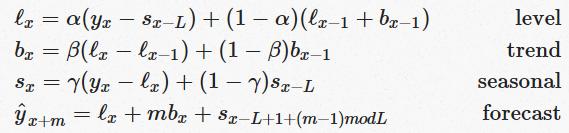
• We now have a third Greek letter, γ (gamma) which is the smoothing factor for the seasonal component.  The forecast equation now consists of level, trend and the seasonal component.

The FORECAST.ETS.SEASONALITY function returns the length of the repetitive pattern Excel detects for the specified time series (s).  FORECAST.ETS.SEASONALITY may be used following FORECAST.ETS to identify which automatic seasonality was detected and used in FORECAST.ETS.  While it can also be used independently of FORECAST.ETS, the functions are tied since the seasonality detected in this function is identical to the one used by FORECAST.ETS, considering the same input parameters that affect data completion.

The FORECAST.ETS.SEASONALITY function employs the following syntax to operate:

The FORECAST.ETS.SEASONALITY function has the following arguments:

• values: this is required.  The values are the historical values, for which you want to forecast the next points
• timeline: this is also required.  This is the independent array or range of numeric data.  The dates in the timeline must have a consistent step between them and cannot be zero (0).  The timeline isn't required to be sorted, as FORECAST.ETS.SEASONALITY will sort it implicitly for calculations.  If a constant step cannot be identified in the provided timeline, FORECAST.ETS.SEASONALITY will return the #NUM! error.  If the timeline contains duplicate values, FORECAST.ETS.SEASONALITY will return the #VALUE! error.  If the ranges of the timeline and values are not of the same size, FORECAST.ETS.SEASONALITY will return the #N/A error
• data_completion: this argument is optional.  Although the timeline requires a constant step between data points, FORECAST.ETS.SEASONALITY supports up to 30% missing data, and will automatically adjust for it.  Zero (0) will indicate the algorithm to account for missing points as zeros.  The default value of 1 will account for missing points by completing them to be the average of the neighboring points
• aggregation: this is the final optional argument.  Although the timeline requires a constant step between data points, FORECAST.ETS.SEASONALITY will aggregate multiple points which have the same time stamp.  The aggregation parameter is a numeric value indicating which method will be used to aggregate several values with the same time stamp.  The default value of 0 will use AVERAGE, while other options are COUNT, COUNTA, MAX, MEDIAN, MIN and SUM.

As an example:

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every other business day.