A to Z of Excel Functions: The DSTDEV Function

Welcome back to our regular A to Z of Excel Functions blog. Today we look at the DSTDEV function.

The DSTDEV function

Imagine you toss an unbiased coin: half of the time it will come down heads, half tails:

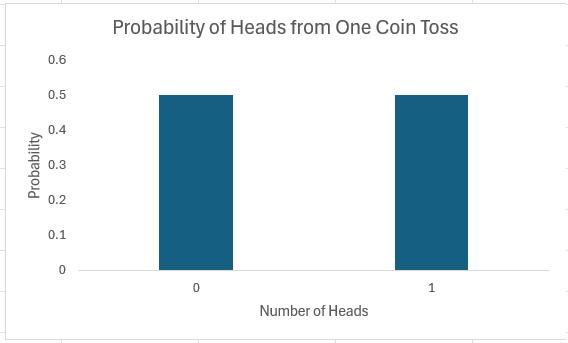
It is not the most exciting chart ever constructed, but it’s a start.

If you toss two coins, there’s four possibilities: two Heads, a Head and a Tail, a Tail and a Head, and two Tails.

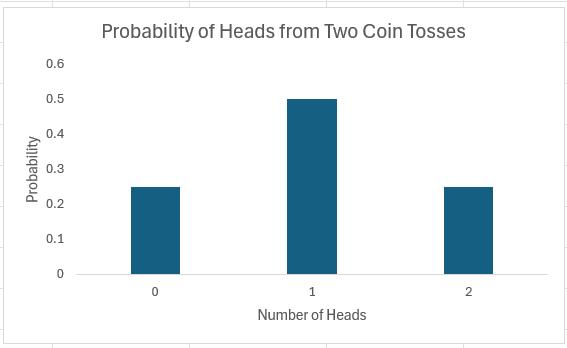
You should get two heads a quarter of the time, one head half of the time and no heads a quarter of the time. Note that (1/4) + (1/2) + (1/4) = 1. These fractions are the probabilities of the events occurring and the sum of all possible outcomes must always add up to 1.

The story is similar if we consider 16 coin tosses say:

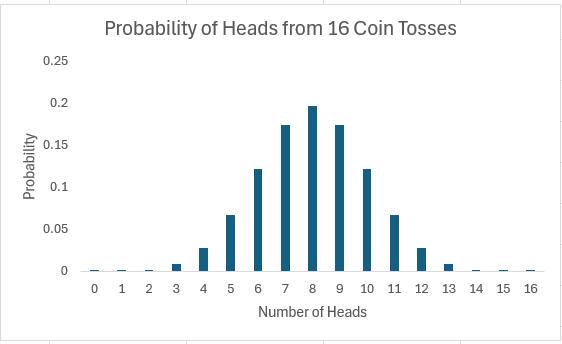
Again, if you were to add up all of the individual probabilities, they would total to 1. Notice that in symmetrical distributions (such as this one) it is common for the most likely event (here, eight heads) to be the event at the midpoint.

Of course, why should we stop at 16 coin tosses?

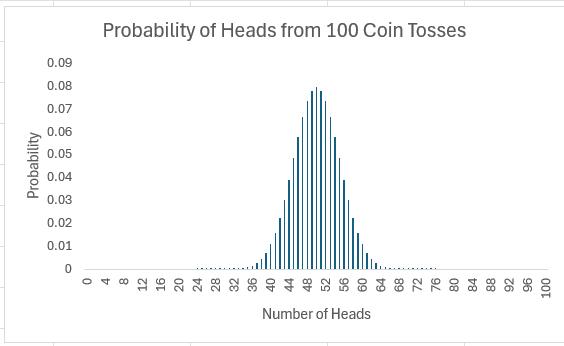
All of these charts represent probability distributions, i.e. it displays how the probabilities of certain events occurring are distributed.  If we can formulate a probability distribution, we can estimate the likelihood of a particular event occurring (e.g. probability of precisely 47 heads from 100 coin tosses is 0.0666, probability of less than or equal to 25 heads occurring in 100 coin tosses is 2.82 x 10^-7, etc.).

Now, I would like to ask the reader to verify this last chart.  Assuming you can toss 100 coins, count the number of heads and record the outcome at one coin toss per second, it shouldn’t take you more than 4.0 X 10²²centuries to generate every permutation.  Even if we were to simulate this experiment using a computer programme capable of generating many calculations a second it would not be possible.  For example, the Japan Times recently announced a new computer that could compute 10,000,000,000,000,000 calculations per second.  If we could use this computer, it would only take us a mere 401,969 years to perform this computation.  Sorry, but I can’t afford the electricity bill.

Let’s put this all into perspective.  All I am talking about here is considering 100 coin tosses.  If only business were that simple.  Potential outcomes for a business would be much more complex.  Clearly, if we want to consider all possible outcomes, we can only do this using some sampling technique based on understanding the underlying probability distributions.

Probability Distributions

If I plotted charts for 1,000 or 10,000 coin tosses similar to the above, I would generate similarly shaped distributions.  This classic distribution which only allows for two outcomes is known as the Binomial distribution and is regularly used in probabilistic analysis.

The 100 coin toss chart shows that the average (or ‘expected’ or ‘mean’) number of heads here is 50.  This can be calculated using a weighted average in the usual way.  The ‘spread’ of heads is clearly quite narrow (tapering off very sharply at less than 40 heads or greater than 60).  This spread is measured by statisticians using a measure called standard deviation which is defined as the square root of the average value of the square of the difference between each possible outcome and the mean, i.e.

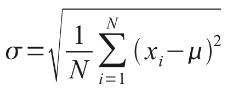
where:

• σ = standard deviation
• N = total number of possible outcomes (for population, or is replaced by n-1, where n is the number of observations in a sample)
• Σ = summation
• x_i = each outcome event (from first x₁ to last x_N) 
• μ = mean or average

The Binomial distribution is not the most common distribution used in probability analysis: that honour belongs to the Gaussian or Normal distribution:

Generated by a complex mathematical formula, this distribution is defined by specifying the mean and standard deviation (see above).  The reason it is so common is that in probability theory, the Central Limit Theorem (CLT) states that, given certain conditions, the mean of a sufficiently large number of independent random variables, each with finite mean and standard deviation, will approximate to a Normal distribution.

The Normal distribution’s population is spread as follow:

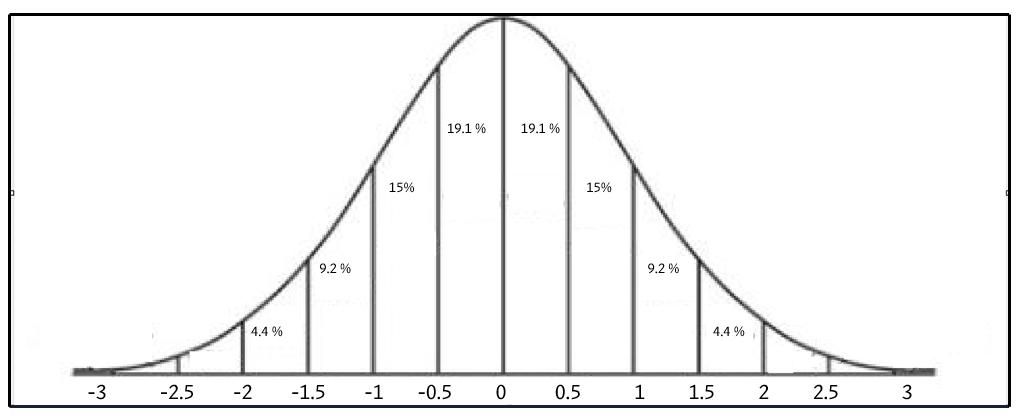
i.e. 68% of the population is within one standard deviation of the mean, 95% within two standard deviations and 99.7% within three standard deviations.

Therefore, if we know the formula to generate the probability distribution – and here I will focus on the Normal distribution – it is possible to predict the mean and range of outcomes using a sampling method. 

For the record, the formula for the Normal distribution is given by

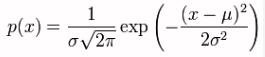
However, here we are concerned about the standard deviation.

The DSTDEV function estimates the standard deviation of a sample by using the numbers in a field (column) of records in a list or database that match conditions that you specify.

The DSTDEV function employs the following syntax to operate:

The DSTDEV function has the following arguments:

• database: this is required and represents the range of cells that makes up the list or database. A database is a list of related data in which rows of related information are records and columns of data are fields. The first row of the list contains labels for each column
• field: indicates which column is used in the function. Make sure you enter the column label enclosed between inverted commas (double quotation marks), e.g. "Age" or "Yield", or a number (without quotation marks) that represents the position of the column within the list, that is, 1 for the first column, 2 for the second column, and so on. Microsoft’s documentation states that this argument is required. We’re not convinced. If field is omitted, DSTDEV calculates the standard deviation of the sample of the records in the table that match the criteria
• criteria: is the range of cells that contains the conditions you specify. You can use any range for the criteria argument, as long as it includes at least one column label and at least one cell below the column label in which you specify a condition for the column.

It should be further noted that:

• you can use any range for the criteria argument, as long as it includes at least one column label and at least one cell below the column label for specifying the condition, e.g. if the range G1:G2 contains the column label Income in G1 and the amount 10,000 in G2, you could define the range as MatchIncome and use that name as the criteria argument in the database functions
• although the criteria range can be located anywhere on the worksheet, do not place the criteria range below the list. If you add more information to the list, the new information is added to the first row below the list. If the row below the list is not blank, Excel cannot add the new information
• make sure that the criteria range does not overlap the list
• to perform an operation on an entire column in a database, enter a blank line below the column labels in the criteria range.

Please see my example below:

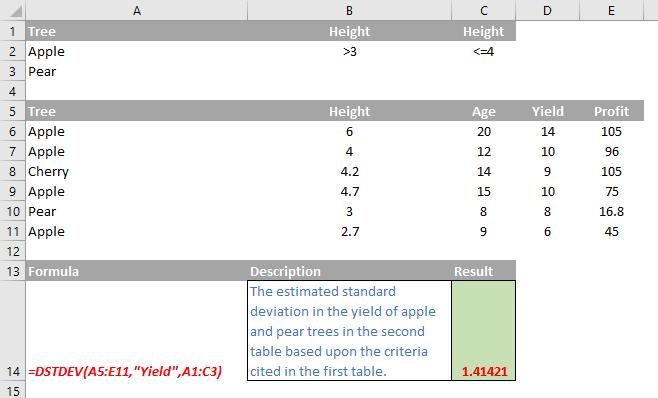
Criteria Examples

Typing an equal sign in a cell indicates you want to enter a formula.  To display text that includes an equal sign, surround the text and the equal sign with double quotes, like so:

"=Liam"

You also do that if you're entering an expression (a combination of formulas, operators, and text) and you want to display the equal sign instead of have Excel use it in a calculation. For example:

=''= entry ''

Where entry is the text or value you want to find.  For example:

• When filtering text data, Excel does not distinguish between uppercase and lowercase characters. However, you can use a formula to perform a case-sensitive search (see below).

The following sections provide examples of complex criteria.

Multiple criteria in one column

Boolean logic: (Salesperson = "Tim" OR Salesperson = "Kathryn")

To find rows that meet multiple criteria for one column, type the criteria directly below each other in separate rows of the criteria range.

e.g. In the following data range (A5:C9), the criteria range (B1:B3) displays the rows that contain either "Tim" or "Kathryn" in the Salesperson column (B5:B9).

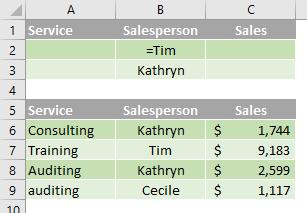
Multiple criteria in multiple columns where all criteria must be true

Boolean logic: (Service = "Auditing" AND Sales > 1500)

To find rows that meet multiple criteria in multiple columns, type all of the criteria in the same row of the criteria range.

In the following data range (A5:C9), the criteria range (A1:C2) displays all rows that contain "Auditing" in the Service column and a value greater than $1,500 in the Sales column (C5:C9).

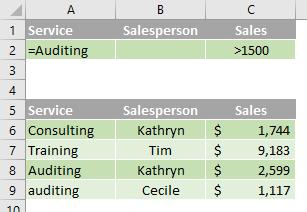
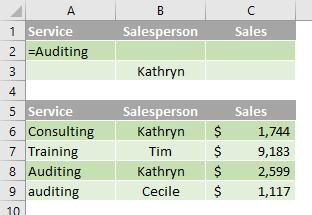
Multiple criteria in multiple columns where any criteria can be true

Boolean logic: (Service = "Auditing" OR Salesperson = "Kathryn")

To find rows that meet multiple criteria in multiple columns, where any criteria can be true, type the criteria in different rows of the criteria range.

In the following data range (A5:C9), the criteria range (A1:B3) displays all rows that contain "Auditing" in the Service column (C5:C9) or "Kathryn" in the Salesperson column (B5:B9).

Multiple sets of criteria where each set includes criteria for multiple columns

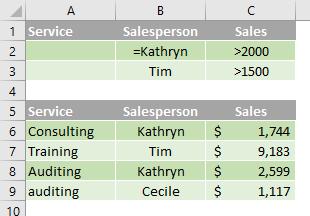
Boolean logic: ( (Salesperson = "Kathryn" AND Sales >2000) OR (Salesperson = "Tim" AND Sales > 1500) )

To find rows that meet multiple sets of criteria, where each set includes criteria for multiple columns, type each set of criteria in separate rows.

In the following data range (A5:C9), the criteria range (B1:C3) displays the rows that contain both "Kathryn" in the Salesperson column and a value greater than $2,000 in the Sales column, or displays the rows that contain "Tim" in the Salesperson column (B5:B9) and a value greater than $1,500 in the Sales column (C5:C9).

Multiple sets of criteria where each set includes criteria for one column

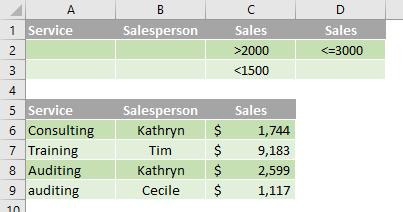
Boolean logic: ( (Sales > 2000 AND Sales <= 3000 ) OR (Sales < 1500) )

To find rows that meet multiple sets of criteria, where each set includes criteria for one column, include multiple columns with the same column heading.

In the following data range (A5:C9), the criteria range (C1:D3) displays rows that contain values between 2,000 and 3,000 and values less than 1,500 in the Sales column (C5:C9).

Criteria to find text values that share some characters but not others

To find text values that share some characters but not others, do one or more of the following:

• type one or more characters without an equal sign (=) to find rows with a text value in a column that begin with those characters. For example, if you type the text Lia as a criterion, Excel finds "Liam", "Liar" and "Lianne"
• use a wildcard character.

The following wildcard characters can be used as comparison criteria:

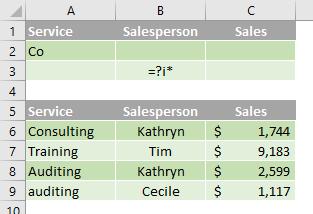
In the following data range (A5:C9), the criteria range (A1:B3) displays rows with "Co" as the first characters in the Service column or rows with the second character equal to "i" in the Salesperson column (B5:B9).

Criteria created as the result of a formula

You can use a calculated value that is the result of a formula as your criterion. Remember the following important points:

• the formula must evaluate to TRUE or FALSE
• because you are using a formula, enter the formula as you normally would, and do not type the expression in the following way:
  
  =''= entry ''
• do not use a column label for criteria labels; either keep the criteria labels blank or use a label that is not a column label in the range (in the examples below, Calculated Average and Exact Match)
• if you use a column label in the formula instead of a relative cell reference or a range name, Excel displays an error value such as #NAME? or #VALUE! in the cell that contains the criterion.  You can ignore this error because it does not affect how the range is filtered
• the formula that you use for criteria must use a relative reference to refer to the corresponding cell in the first row (in the examples below, C6 and A6)
• all other references in the formula must be absolute references.

The following subsections provide specific examples of criteria created as the result of a formula.

Filtering for values greater than the average of all values in the data range

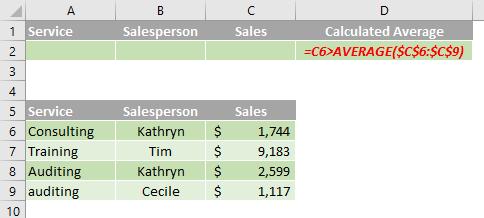
In the following data range (A5:C9), the criteria range (D1:D2) displays rows that have a value in the Sales column greater than the average of all the   values (C6:C9). In the formula, "C6" refers to the filtered column (C) of the first row of the data range (6).

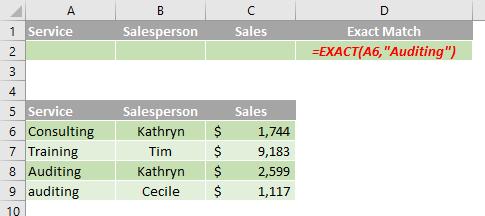
Filtering for text by using a case-sensitive search

In the data range (A5:C9), the criteria range (D1:D2) displays rows that contain "Auditing" in the Service column by using the EXACT function to perform a case-sensitive search (A5:A9).  In the formula, "A6" refers to the filtered column (A) of the first row of the data range (6).

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every business day.

A full page of the function articles can be found here.