A to Z of Excel Functions: The COSH Function

The COSH function

You probably think we talk a load of hyperbolics here, but that’s what happens when we are under the COSH. This function returns the hyperbolic cosine of a number.

That’s all well and good if you know what “hyperbolic cosine” means. In mathematics, hyperbolic functions are analogous to the trigonometric, or circular, functions, such as sine and cosine.

Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh z, sinh z) form the right half of the equilateral hyperbola (please see the figure below). The hyperbolic functions take a real argument called a hyperbolic angle. The size of a hyperbolic angle is twice the area of its hyperbolic sector. The hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector.

Hyperbolic functions occur in the solutions of many linear differential equations, such as some cubic equations. Further, in complex analysis, the hyperbolic functions arise as the imaginary parts of sine and cosine – but that’s a story for another day.

The COSH function employs the following syntax to operate:

The COSH function has the following arguments:

• number: this is required and represents any real number for which you want to find the hyperbolic cosine.

It should be further noted that the formula for the hyperbolic cosine is:

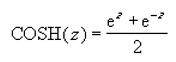
Please see my example below:

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every other business day.

A full page of the function articles can be found here.