A to Z of Excel Functions: The CONFIDENCE Function
25 September 2017
Welcome back to our regular A to Z of Excel Functions blog. Today we look at the CONFIDENCE function.
The CONFIDENCE function
Do you need more CONFIDENCE in your Excel files? This function returns the confidence interval for a population mean, using the theory associated with the normal distribution.
To explain: the confidence interval is a range of values around a sample mean, x, which sits at the centre of this range, i.e. the range is x ± CONFIDENCE. For example, if x is the sample mean of delivery times for products ordered through the mail, x ± CONFIDENCE is a range of population means.
For any population mean, μ0, in this range, the probability of obtaining a sample mean further from μ0 than x is greater than the significance level required, alpha; for any population mean, μ0, not in this range, the probability of obtaining a sample mean further from μ0 than x is less than this level, alpha. In other words, assume that we use x, a standard deviation standard_dev, and size to construct a two-tailed test at significance level alpha of the hypothesis that the population mean is μ0. Then we will not reject that hypothesis if μ0 is in the confidence interval and will reject that hypothesis if μ0 is not in the confidence interval. The confidence interval does not allow us to infer that there is probability 1 – alpha that our next package will take a delivery time that is in the confidence interval.
The CONFIDENCE function employs the following syntax to operate:
CONFIDENCE(alpha, standard_dev, size)
- alpha: this is required. This represents the significance level used to compute the confidence level. The confidence level equals 100*(1 - alpha)%, or in other words, an alpha of 0.05 indicates a 95 percent confidence level
- standard_dev: this is also required. This is the population standard deviation for the data range and is assumed to be known
- size: also required. This is the sample size.
It should be further noted that:
- if any argument is non-numeric, CONFIDENCE returns the #VALUE! error value
- if alpha is ≤ 0 or ≥ 1, CONFIDENCE returns the #NUM! error value
- if standard_dev ≤ 0, CONFIDENCE returns the #NUM! error value
- if size is not an integer, it is truncated
- if size < 1, CONFIDENCE returns the #NUM! error value
- if we assume alpha equals 0.05, we need to calculate the area under the standard normal curve that equals 1 - alpha, or 95%. This value is ± 1.96. The confidence interval is therefore:
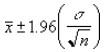
Please see my example below:

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every other business day.

