A to Z of Excel Functions: The CHIINV Function

Welcome back to our regular A to Z of Excel Functions blog.  Today we look at the CHIINV function.

The CHIINV function

In probability theory and statistics, the chi-squared distribution (also chi-square or χ2-distribution) with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables.  It is one of the most widely used probability distributions in inferential statistics, e.g. in hypothesis testing or in construction of confidence intervals. 

The chi-squared distribution is used in the common chi-squared tests for goodness of fit of an observed distribution to a proposed theoretical one, the independence of two criteria of classification of qualitative data, and in confidence interval estimation for a population standard deviation of a normal distribution from a sample standard deviation.

If Z₁, ..., Z_k are independent, standard normal random variables, then the sum of their squares

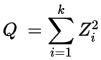
is distributed according to the chi-squared distribution with k degrees of freedom.  This is usually denoted as

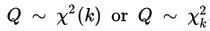
Thus, the chi-squared distribution has one parameter: k — a positive integer that specifies the number of degrees of freedom.

As aforementioned, the chi-squared distribution is used primarily in hypothesis testing.  Unlike more widely known distributions such as the normal distribution and the exponential distribution, the chi-squared distribution is rarely used to model natural phenomena.  It arises in the following hypothesis tests, among others.

The primary reason that the chi-squared distribution is used extensively in hypothesis testing is its relationship to the normal distribution.  Many hypothesis tests use a test statistic, such as the t statistic in a t-test.  For these hypothesis tests, as the sample size, n, increases, the sampling distribution of the test statistic approaches the normal distribution (Central Limit Theorem).  Since the test statistic (such as t) is asymptotically normally distributed, provided the sample size is sufficiently large, the distribution used for hypothesis testing may be approximated by a normal distribution.  Testing hypotheses using a normal distribution is well understood and relatively easy.  The simplest chi-squared distribution is the square of a standard normal distribution.  So wherever a normal distribution could be used for a hypothesis test, a chi-squared distribution could be used.

A chi-squared distribution constructed by squaring a single standard normal distribution is said to have 1 degree of freedom, etc.

The CHIINV function returns the inverse of the right-tailed probability of the chi-squared distribution.  If probability = CHIDIST(x,...), then CHIINV(probability,...) = x.  This function may be used to compare observed results with expected ones in order to decide whether your original hypothesis is valid.

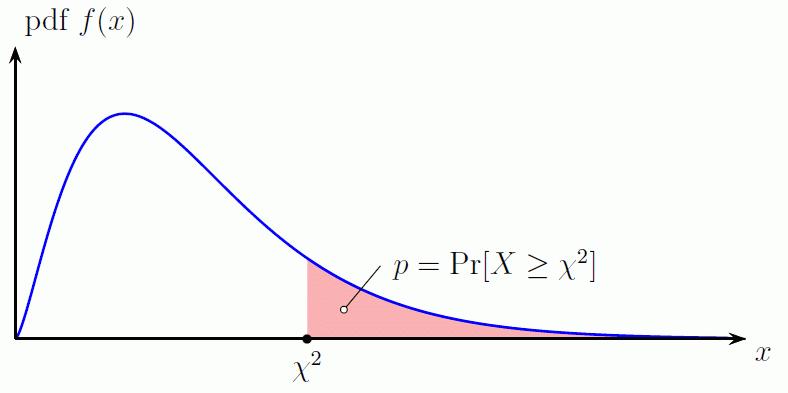
The CHIINV function employs the following syntax to operate:

The CHIINV function has the following arguments:

• probability: this is required and represents a probability associated with the chi-squared distribution
• deg_freedom: this is also required. This represents the number of degrees of freedom.

It should be further noted that:

• if either argument is nonnumeric, CHIINV returns the #VALUE! error value
• if probability < 0 or probability > 1, CHIINV returns the #NUM! error value
• if deg_freedom is not an integer, it is truncated
• if deg_freedom < 1, CHIINV returns the #NUM! error value

It should be noted that this function has been replaced with one or more new functions from Excel 2010 onwards (CHISQ.INV.RT) that may provide improved accuracy and whose names better reflect their usage.  Although this function is still available for backward compatibility, you should consider using the new functions from now on, because this function may not be available in future versions of Excel.  This may require you to amend existing models too.

Given a value for probability, CHIINV seeks that value x such that CHIDIST(x, deg_freedom) = probability.  Thus, the precision of CHIINV depends on the precision of CHIDIST. CHIINV uses an iterative search technique.  If the search has not converged after a maximum of 100 iterations, the function returns the #N/A error value.

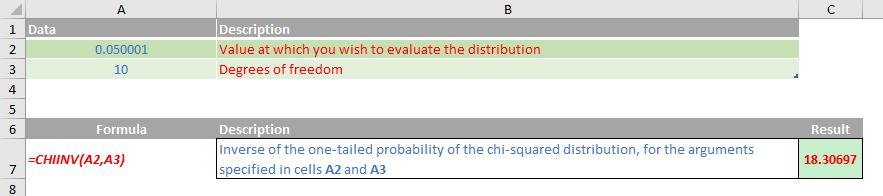
Please see my example below:

We’ll continue our A to Z of Excel Functions soon.  Keep checking back – there’s a new blog post every other business day.