A to Z of Excel Functions: The BINOM.DIST.RANGE Function

Welcome back to our regular A to Z of Excel Functions blog.  Today we look at the BINOM.DIST.RANGE function.

The BINOM.DIST.RANGE function

In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent success / failure experiments, each of which yields success with probability p.  For the record, a success / failure experiment is also called a Bernoulli experiment or Bernoulli trial.  The binomial distribution is frequently used to model the number of successes in a sample of size n drawn with replacement from a population of size N.

This function returns the probability of a trial result using a binomial distribution.

The BINOM.DIST.RANGE function employs the following syntax to operate:

The BINOM.DIST.RANGE function has the following arguments:

• trials: this is required and represents the number of independent trials.  The value must be greater than or equal to 0
• probability_s: this is also required.  This is the probability of success in each trial.  This must be greater than or equal to 0 and less than or equal to 1, just like every probability
• number_s: again, required.  This is the number of successes in trials.  This must be greater than or equal to 0 and less than or equal to trials
• number_s2: this argument is optional.  If it is provided, this returns the probability that the number of successful trials will fall between number_s and number_s2.  Must be greater than or equal to number_s and less than or equal to trials.

It should be further noted that:

• if any arguments are outside of their constraints, BINOM.DIST.RANGE returns the #NUM! error value
• if any arguments are non-numeric values, BINOM.DIST.RANGE returns the #VALUE! error value
• the following equation is used:

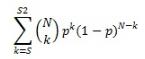
• in the equation above, N is trials, p is probability_s, s is number_s, s2 is number_s2, and k is the iteration variable
• numeric arguments are truncated to integers.

Please see my example below:

We’ll continue our A to Z of Excel Functions soon.  Keep checking back – there’s a new blog post every other business day.