A to Z of Excel Functions: The BESSELY Function
14 November 2016
Welcome back to our regular A to Z of Excel Functions blog. Today we look at the BESSELY function.
The BESSELY function
Bessel functions were first defined by the mathematician Daniel Bernoulli and then generalised by Friedrich Bessel as the canonical solutions y(x) of the differential equation
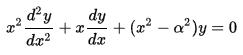
(known as Bessel's differential equation) for an arbitrary complex number α, the order of the Bessel function. Although α and −α produce the same differential equation for real α, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of α.
This is not meant to be a mathematical lecture. I will be out of my depth very quickly. Essentially, Excel has four modified Bessel functions, which may be used by specialists as and when needed. BESSELY returns the Bessel function, which is also called the Weber function or the Neumann function.
The BESSELY function employs the following syntax to operate:
BESSELY(x, n)
The BESSELY function has the following arguments:
- x: required. The value at which to evaluate the function.
- n: also required. The order of the function. If n is not an integer, it is truncated accordingly.
It should be further noted that:
- If x is nonnumeric, BESSELY returns the #VALUE! error value
- If n is nonnumeric, BESSELY returns the #VALUE! error value
- If n < 0, BESSELY returns the #NUM! error value
- The nth order Bessel function of the variable x is:
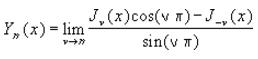
where Jv is the BESSELJ function and the others are the usual trigonometric functions.
Please see yet another highly informative example below:

We’ll continue our A to Z of Excel Functions soon. Keep checking back – there’s a new blog post every other business day.

